Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 612345789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Calcule a área delimitada entre as curvas:

y = 1 x         ;           y = x           ;           y = x 4           ;           x > 0

Passo 1

Vamos lá desenhando a região primeiro. Vou começar pelo y = 1 / x :

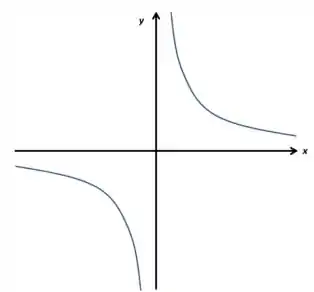
Bom, esse é o desenho base desse gráfico, que tem forma de hipérbole. Agora vou pensar em como encaixar os outros. Ora, tenho que ver aonde eles se interceptam! Primeiro o y = x :

y = x   vermelho         ;           y = 1 x   (azul)

x = 1 x       →           x 2 = 1       →           x = ± 1

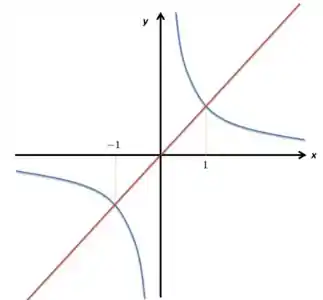
Agora, eu vou botar o outro, o y = x / 4 :

y = x 4 verde         ;           y = 1 x (azul)

x 4 = 1 x       →           x 2 = 4       →           x = ± 2

Além de que ela toca a y = x quando x = 0 :

y = x   (vermelho)         ;           y = x 4 (verde)

x = x 4       →         3 x 4 = 0     →           x = 0

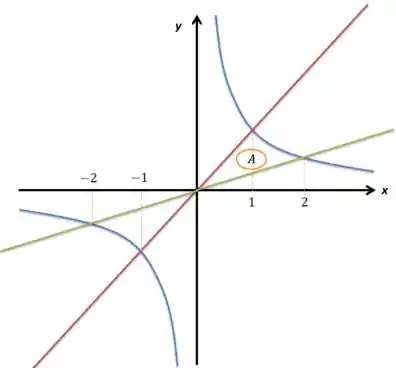
Então essa área entre os 3 gráficos está aí marcada com A . Lembrando que até teria uma outra área ali embaixo entre os gráficos, só que o cara especificou que x > 0 .

Então, a integral está rolando de 0 até 2 , sendo que até o 1 nós temos vermelho por cima e verde por baixo e a partir daí temos azul em cima e verde embaixo, ou seja:

∫ a b f cima - f baixo d x = ∫ 0 1 f Vermelho - f verde d x + ∫ 1 2 f azul - f verde d x

A = ∫ 0 1 x - x 4 d x + ∫ 1 2 1 x - x 4 d x

Passo 2

Agora vamos integrar!

∫ 0 1 x - x 4 d x = ∫ 0 1 3 x 4 d x = 3 x 2 8 [ 1 0 = 3 8

∫ 1 2 1 x - x 4 d x = ln ⁡ x - x 2 8 [ 2 1 = ln ⁡ 2 - 3 8

∫ 0 1 x - x 4 d x + ∫ 1 2 1 x - x 4 d x = 3 8 + ln ⁡ 2 - 3 8 = ln ⁡ 2

Resposta

A = ln ⁡ 2

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x