Área entre Curvas
Os gráficos de
Se interceptam quatro vezes, limitando duas regiões. Encontre a área dessas regiões.
Passo 1
Vou começar ignorando o esboço delas e a disposição dessas regiões aí. Vou começar igualando esses cara para que a gente veja onde se interceptam.
Vamos por Bhaskara:
Assim, os valores de serão:
Achamos os nossos interceptos.
Passo 2
Pensando em como desenhar, temos uma parábola no e um gráfico hiperbólico no . A gente repara inclusive que ambos gráficos são espelhados em relação ao eixo , é a chamada função par, em que para todo . Vamos então esboçar esse negócio levando em conta os pontos que achamos em que eles se interceptam:
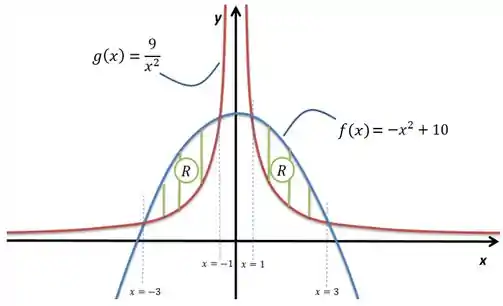
Como dá para ver, A região limitada entre os dois gráficos é dada pelos dois ’s ali. Agora, bem como os gráficos, as regiões serão simétricas em relação ao eixo . Então a área total pode ser calculada como duas vezes uma das áreas: