Questão 4: Sabe-se que as curvas e intersectam-se em exatamente três pontos com abscissas , e , respectivamente, onde é um número real negativo.
Calcule a área total, em termos de , da região entre as curvas para .
Dica: Faça um esboço destacando os pontos importantes e lembre-se que .
Passo 1
Eu sei, dá vontade de encontrar aquele neh? Mas não, não é isso que queremos. Na verdade queremos que a área esteja em termos de . Bem, a primeira coisa aqui é desenhar a região que queremos a área, assim como a dica nos disse:
1º - A curva (Uma parábola)
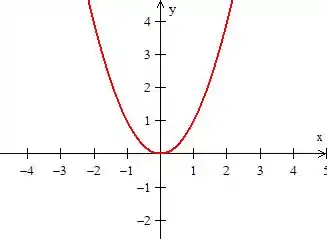
2º - A exponencial (Uma exponencial semelhante ao gráfico de ):
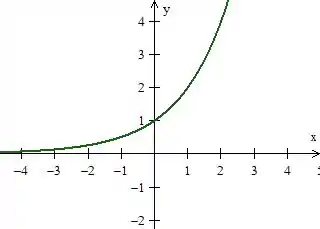
Logo, essas duas coisas juntas nos dá...
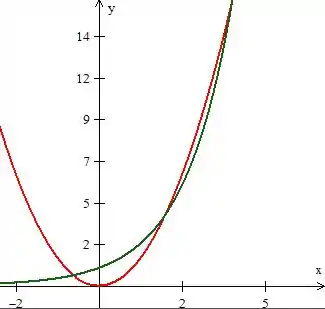
Repare que em , e , temos de fato o encontro dessas coisas. Queremos a área entre elas de a , logo a área da região...
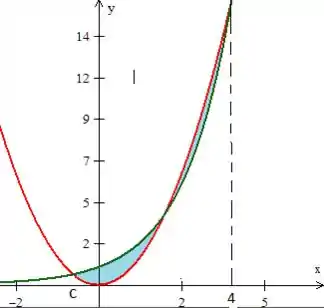
Passo 2
Área de superfície é sempre dada pela fórmula:
Onde e são os pontos de variação de da área. é a função que está por cima e a que está por baixo!
Para a área da nossa região de até ,
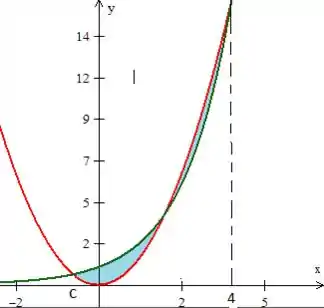
precisamos separar em duas partes e calcular a área desses gomos separados e depois somar tudo.
Passo 3
Para a área do primeiro gomo, de até , usamos...
Onde a função que esta por cima no caso é a exponencial e a de baixo é a parábola:
Para essa outra integral, ela não tem uma integral direta. Mas, se pegarmos a dica...
Agora sim a integral é direta...
Eis a área do primeiro gomo ;)
Passo 4
Quanto á área do segundo gomo usamos a mesmíssima fórmula...
A diferença é que agora vamos considerar e
a função de cima é a parábola e a de baixo a função exponencial...
A primitiva dessas duas já foram encontradas no passo anterior...
Passo 5
Somando então essas duas áreas, encontramos a área de que queríamos...
Como pela dica, temos ...
Bem, note que esse valor é negativo, afinal também é negativo, logo, a área na real é o módulo desses valores...