UFSC, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFSC - Lista 2.1 - Áreas entre curvas, Questão P1a
Em cada item, determine a área da região sombreada.
Passo 1
Fala, galera! Vamos resolver essa questão!
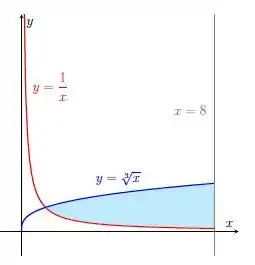
O enunciado pediu pra gente determinar a área entre as curvas de , e , que é a nossa área em azul. O primeiro limite horizontal é definido na interseção entre as curvas, ou seja, para:
Verificando os limites horizontais, vamos ter os limites de integração da integral de área da região, que vai ser dada pela diferença entre a função que está em cima e a função que está embaixo, ou seja:
Onde, nesse caso, e .
Vamos lá!
Passo 2
Vamos começar descobrindo o ponto onde as curvas se interseptam, fazendo:
Elevando os dois lados ao cubo:
Como nossa região tá no primeiro quadrante, vamos escolher apenas o positivo. Assim, sabemos que a região é limitada horizontalmente por e e podemos montar nossa integral:
Separando a integral da diferença na diferença das integrais, temos:
Usando a regrinha da potência para integrar () o primeiro termo e sabendo que , temos:
Como , vamos obter:
Calculando as raízes e usando as propriedades do logaritmo:
Valeu, galera! Até a próxima! 😉