Calcule a área delimitada entre as curvas:
Passo 1
Começamos desenhando as duas parábolas:
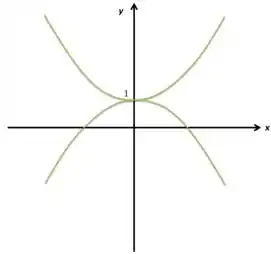
Ok, até aí sem muitos problemas. Agora que devemos encaixar aquela reta ali as devidas interseções. Bom, se você igualar esse gráfico ao gráfico da parábola superior, olha como fica:
Bom, se eu adicionar ainda o gráfico uma vertical paralela ao eixo passando em :
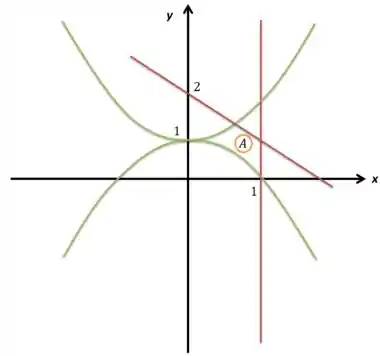
Já tenho ali a minha área definida, então.
Bom, agoraeu só preciso analisar o seguinte:
de até eu tenho a parábola de cima sobre a parábola de baixo
de até tenho a reta não vertical em cima da parábola de baixo. Assim:
Passo 2
Integrando uma de cada vez:
Passo 3
Agora a segunda parte
Passo 4
Juntando tudo
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x