UFSC, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFSC - Lista 2.1 - Áreas entre curvas, Questão P1c
Em cada item, determine a área da região sombreada.
Passo 1
Fala, galera! Vamos resolver essa questão!
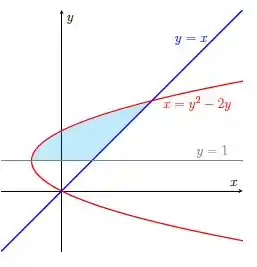
O enunciado pediu pra gente determinar a área entre as curvas de , e , que é a nossa área em azul. Repare que as funções são colocada em relação a , então vamos ter uma integral de área em relação a .
Os limites horizontais são definidos pelas duas curvas e os limites verticais vão ser definidos pelas constantes, em e no ponto de interseção entre as curvas.
Verificando os limites verticais, vamos ter os limites de integração da região, que vai ser dada pela diferença entre a função que está a direita e a função que está a esquerda, ou seja:
Onde, nesse caso, e .
Vamos lá!
Passo 2
Vamos começar descobrindo o ponto onde as curvas se interseptam lá em cima, fazendo:
Então, os gráficos se tocam em . Como o enunciado também definiu a reta como um limite vertical, nossos limites estão no intervalo .
Passo 3
Montando nossa integral de área:
Com e , temos:
Usando a regrinha da potência para integrar (), vamos obter:
Aplicando os limites de integração:
Valeu, galera! Até a próxima! 😉