Determine a área da figura plana delimitada pelos gráficos de e e pelas retas e .

Vou desenhar o gráfico da região. Só tem um detalhe, não sei fazer aquele gráfico do . Bom, eu sei mais ou menos como é , algo assim:

Bom, então se eu pegar isso e multiplicar por vou ter isso só que mais apertado horizontalmente e espelhado em relação ao eixo . Somando basta eu andar tudo uma casa acima, sabendo ainda que tenho apenas uma raiz:

O eu sei desenhar, então vamos para o esboço logo:

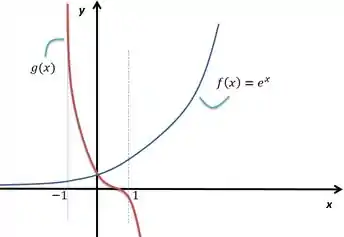
No intervalo de até o é maior que . A partir daí eles se invertem. Vamos escrever a integral com essas informações:

Agora é só resolver!