Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 631234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos dar uma olhada em como ficaria o gráfico dessas funções.

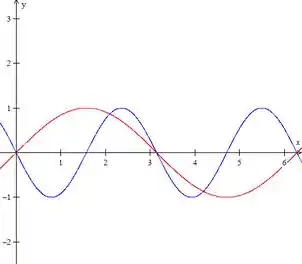
A curva em azul é y = - sen ⁡ 2 x   e em vermelho y = sen ⁡ ( x ) .

Igualando as curvas, vemos que no intervalo entre 0 e π , as funções se encontram em 3 pontos:

sen ⁡ x = - sen ⁡ ( 2 x )

x = 0  

x = π

x = 2 π 3

Passo 2

Para calcular a área entre as curvas vamos fazer a integral. Entre 0   e 2 π 3 a curva de cima é y = sen ⁡ x , então

∫ 0   2 π 3 sen ⁡ ( x ) - - sen ⁡ 2 x d x

E entre   2 π 3 e π , a curva por cima é y = - sen ⁡ 2 x .   Logo,

∫   2 π 3 π - sen ⁡ 2 x - sen ⁡ ( x ) d x

Então a área entre as curvas será

A = ∫ 0   2 π 3 sen ⁡ ( x ) + sen ⁡ ( 2 x ) d x + ∫   2 π 3 π - sen ⁡ 2 x + sen ⁡ x d x

Passo 3

Integrando ficamos com

A = - cos ⁡ x - 1 2 cos ⁡ 2 x 0   2 π 3 + 1 2 cos ⁡ 2 x + cos ⁡ x   2 π 3 π

A = - cos ⁡   2 π 3 + cos ⁡ 0 - 1 2 cos ⁡   4 π 3 + 1 2 cos ⁡ 0 + 1 2 cos ⁡ ( 2 π ) - 1 2 cos ⁡   4 π 3 + c o s ⁡ ( π ) - cos ⁡   2 π 3

A = 5 2

Resposta

∫ 0 2 π 3 sen ⁡ x + sen ⁡ 2 x d x + ∫ 2 π 3 π - sen ⁡ x + sen ⁡ 2 x d x = 5 2

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x