Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 701234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre Curvas

( a ) Calcule a área da região

A = x , y ∈   R 2 : x > 0 ,   y ≤ 1 , 1 x ≤ y ≤ 4 x 2

Passo 1

Sabemos que estamos numa região onde x > 0 e y ≤ 1 . Pensando nas duas curvas entre as quais y se encontra vamos ver se existem pontos onde os gráficos se encontram:

1 x = 4 x 2 ,       p a r a   x ≠ 0

x 2 - 4 x = 0

x = 0 ; x = 4

Como x = 0 não é parte do domínio das funções, seu único ponto de encontro é em x = 4 . Vamos agora desenhar as duas hipérboles na região trabalhada:

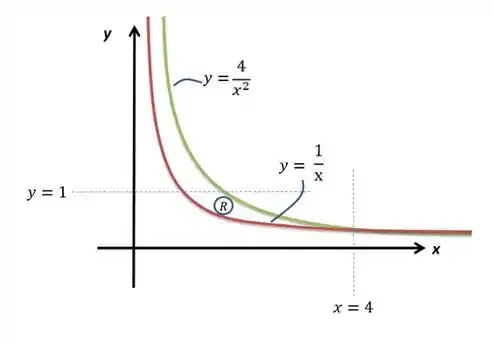
Passo 2

Repara numa coisa, a forma mais prática de trabalhar a integral para a área seria invertendo a função e integrando do ponto onde elas se encontram y = 4 4 2 = 1 4 até y = 1 . As inversas de y = 1 x e de y = 4 x 2 serão:

x = 1 y = y - 1   ;   x = 2 y = 2 y - 1 2

Assim, a área é aquela compreendida entre o gráfico vermelho, inferiormente, e o gráfico verde, superiormente, de y = 1 4 até y = 1 (lembre-se que

A = ∫ 1 4 1 2 y - 1 2 - 1 y d y

A = 2 ∙ 2   y 1 2 - ln ⁡ y y = 1 4 y = 1 = 4 y - ln ⁡ y y = 1 4 y = 1

A = 4 1 - ln ⁡ 1 - 4 1 4 - ln ⁡ 1 4

A = 4 - 0 - 4 1 2 - ln ⁡ 2 - 2

A = 4 - 2 - ln ⁡ 2 - 2

A = 4 - 2 + ln ⁡ 2 - 2

A = 2 + ln ⁡ 2 - 2

Por propriedade de logarítimo...

A = 2 - 2 ln ⁡ 2

Resposta

A = 2 - 2 ln ⁡ 2   u . a .

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x