Encontre a área da região limitada por , e .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Para essa questão, foi dada três equações e nosso objetivo é obter a área limitada pelo gráfico dessas três equações.
As equações em questão são dadas por , e .
Todas essas são bastante utilizadas no nosso cotidiano.
Então como calculamos a área entre essas equações? 🤔
A ideia de cálculo de área está estritamente relacionada com o cálculo de integral.
A integral da área é dada como
Onde é os limites de integração da área.
Vamos analisar a área entre os gráficos para analisar como podemos calcular essa integral.
Bora lá! 😁
Passo 2
Esboçando os gráficos de (Vermelha) e (Azul), e isolando em , temos (Roxa), facilitando a visualização do gráfico.
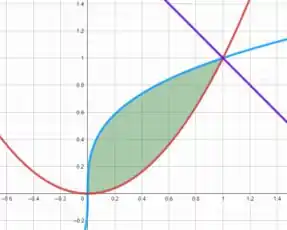
Vemos que nossa área de interesse é a área hachurada de verde.
Perceba que o limite superior da área é dada pela equação já o limite inferior é dada pela equação .
Vamos isolar na primeira equação para deixar as duas em função de
Montando nossa integral como o limite superior como e o inferior como , vamos obter
Agora para a outra integral, temos que aplicar os limites de integração baseado na variação que faz na área.
Pelos pontos de intercessão das curvas e pela imagem da área que estamos interessados, vemos que está variando no intervalo de a . Logo os limites de integração para será
Prontinho! Bora começar! 🤩
Passo 3
A primeira integral é a integral de com relação a , ou seja, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração.
Aplicando os limites de integração
Agora integramos o resultado com relação a
Pelo método de integração polinomial, temos
Aplicando os limites de integração
Dessa forma, o resultado da nossa integral e consequentemente da área que estávamos interessados é igual a
Interessante, não é? 😎
Fim! Iae, o que achou? Responde Aí! 😁
