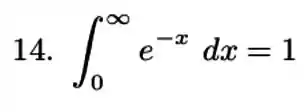![]()
Passo 1
O primeiro quadrante tem
Para calcular a região abaixo da curva e no primeiro quadrante precisamos resolver a integral
Passo 2
Esta é uma integral imprópria, para resolve-la, precisamos aplicar o limite
E resolver a integral normalmente
E aplicando os limites de integração
Voltando para o limite
A área da região no primeiro quadrante e abaixo da curva é 1.
Resposta