Questão 4) Considere as funções e . Calcule a área da região limitada pelos gráficos de e no intervalo .
Passo 1
Bem, antes de passarmos para o problema da área em si, vamos desenhar essa região para ver com quem a gente está lidando, ok?
A curva de trata-se da função raiz, e a outra a função cúbica...
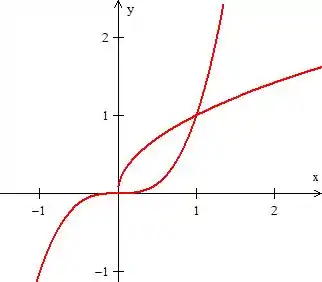
Perceba que essas funções se cruzam exatamente em e , pois...
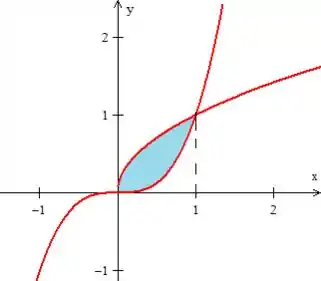
Passo 2
Para a determinação da área de , saiba que uma área aqui sempre será dada por...
Onde é a função que está por cima e , a função que está por baixo.
Onde a função de cima é e curva de baixo até é a ...
Passo 3
Agora é só calcular!
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x