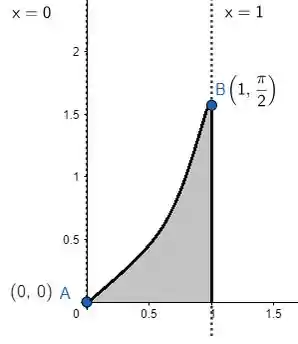
3) Considere a região plana
- Esboce a região
- Escreva a área de como uma integral na variável
- Calcule a área da região utilizando o método que preferir
Passo 1
Questão de esboço de gráfico? Errr, masomenos! Essa questão quer mais que a gente saiba calcular área entre curvas do que que a gente saiba esboçar com precisão esse gráfico. Então vamos prestar atenção em algumas coisas sobre :
Opa, se isso ta valendo, então a função só pode existir ou no primeiro ou no quarto quadrante:
Ok, mas não tem gráfico ainda aí! Calma gafanhoto, vamos olhar pro outro pedaço da região :
Oras! Se está entre e uma função, então na prática queremos algo no primeiro quadrante! Esquece o quarto! E como os limites de foram dados, temos que:
E logo o gráfico vai ficar:
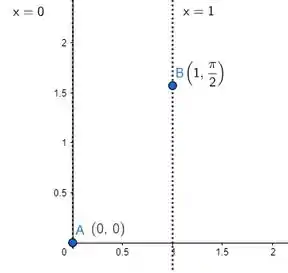
Cara, ainda não tem gráfico aí! Mas olha só, sabemos que temos que ligar os pontos A e B! O jeito vai ser descobrir o como! Pra isso, vamos olhar a função:
É uma inversa trigonométrica, certo? Então se olharmos pro círculo trigonométrico:
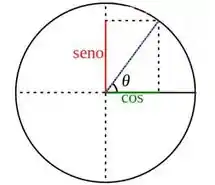
Veja bem, conforme aumentamos o arco (ou seja, ), partindo de , aumentamos sempre ! só passa a diminuir se o arco passar de , o que a gente nem precisa se preocupar já que a curva está limitada exatamente para esse valor do arco. Oras, então é uma função estritamente crescente! E como pra valores muito pequenos de arco a gente tem senos muito próximos de 0, uma concavidade pra cima cai bem em! Vamos esboçar então:
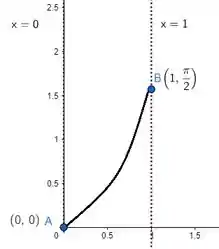
E a região vai ser:
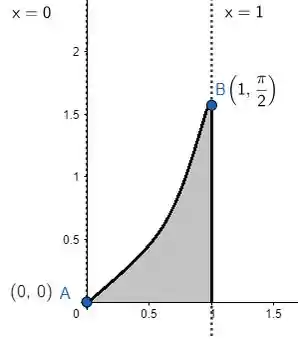
Passo 2
Agora bora tentar achar a área desse cara. Pra isso, vamos lembrar que a questão pede em ! Se:
Então:
E se os valores de eram limitados por:
Oras, então os valores de que limitam são os valores que dão esses senos, logo:
Mas calma lá, a integral não vai ser bem exatamente:
Que talvez seja intuitivo pra gente responder. Temos que ter cuidado, porque quando invertemos uma função, o que estamos fazendo é na verdade girar ela 90º no sentido anti-horário e depois espelhando com a vertical:
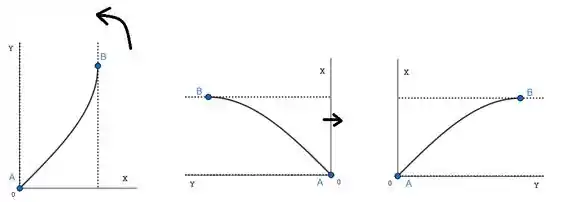
A primeira curva é nosso e a terceira, . Ou seja, nossa curva esboçada vai ser:
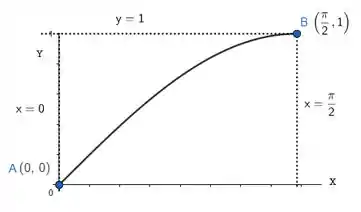
Só que a região nessa figura aí, vai ser:
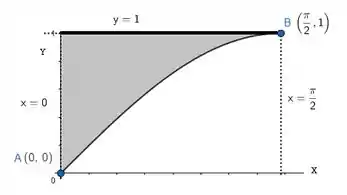
E veja bem, isso não é lá a integral que a gente ia por em! A integral que íamos por era na verdade essa área:
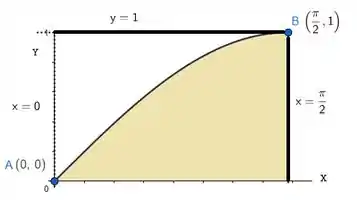
O que fazer agora? Olha só a sagacidade, se fizermos a integral:
Vamos ter, na verdade, a seguinte área:
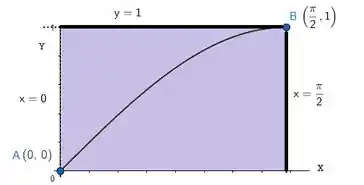
Opa, então pra achar a cinza basta pra gente então subtrair da roxa a bege, vamos ter então::
Passo 3
Pra fechar a questão e partir pro abraço, basta a gente resolver o cálculo da integral em! Então bora lá: