Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 921234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909193949596979899100

Enunciado

UFSC – Cálculo 1 – Lista 4.3 – Questão 5a – Parte 2

f e g representadas abaixo. Em cada região marcada, está indicada a medida da área

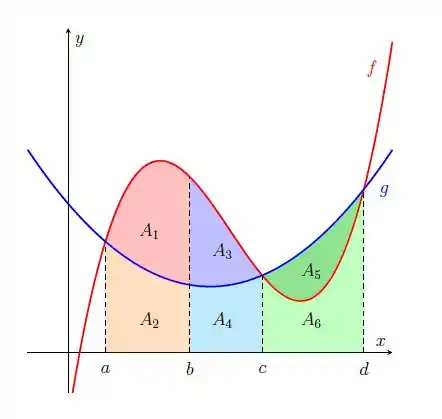
  1. Escreva o resultado das integrais   ∫ a b g ( x ) d x ,   ∫ b c g ( x ) d x   e   ∫ c d g ( x ) d x em termos das medidas das áreas

Passo 1

E aí pessoal, tudo bem?

Essa questão é uma continuação! Na primeira parte o problema pediu para calcularmos essas mesmas integrais, mas agora olhando para a função f ( x ) . Agora vamos repetir o raciocínio para a g ( x ) .

g ( x ) que está em azul

Tudo bem até aqui?

Mas relaxa, vou fazer passo a passo com você!

Passo 2

Vamos começar escrevendo o resultado dessa integral aqui

∫ a b g ( x ) d x

Os intervalos são de x = a até x = b :

g ( x ) é exatamente a área A 2 , então podemos escrever essa integral assim:

∫ a b g ( x ) d x = A 2

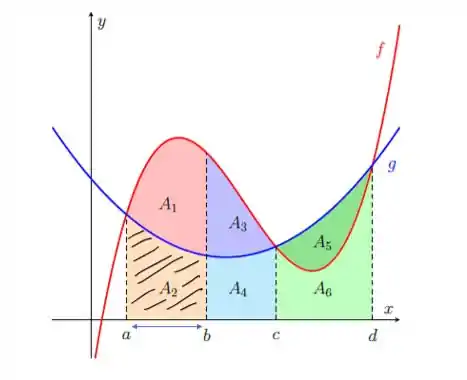
Tranquilo?

Passo 3

Agora vamos escrever essa integral aqui

∫ b c g ( x ) d x

Agora vamos olhar os intervalos de x = b até x = c :

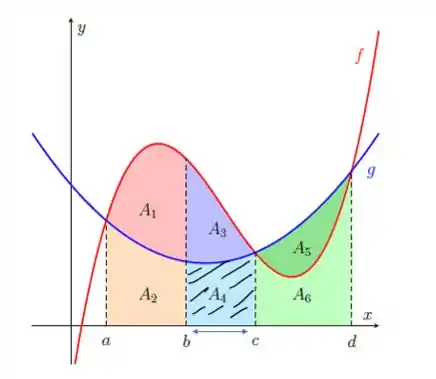
A área abaixo da curva g ( x ) é exatamente a área A 4 , então podemos escrever essa integral assim:

∫ b c g ( x ) d x = A 4

Beleza? Vamos para a última integral?

Passo 4

Agora o último intervalo a ser considerado:

∫ c d g ( x ) d x

É de x = c até x = d , sempre olhando abaixo da curva g ( x ) :

A 5 e A 6 ! Então a integral de g ( x ) nesse intervalo será a SOMA dessas duas áreas:

∫ c d g ( x ) d x = A 5 + A 6

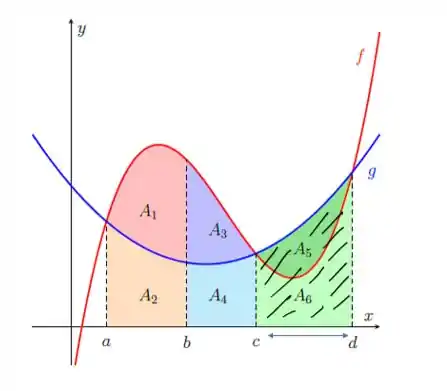
E é isso! Terminamos a questão!

Espero ter ajudado! Vamos para a próxima?

Resposta

∫ a b g ( x ) d x = A 2

∫ b c g ( x ) d x = A 4

∫ c d g ( x ) d x = A 5 + A 6

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x