Seja a região limitada entre e o eixo . Encontre a equação da reta que passa pela origem e que divide em duas subregiões com áreas iguais.
Passo 1
Ora, ora. Problema interessante...
Foi nos dada uma função parabólica (do 2º grau e com concavidade para baixo). Essa curva e o eixo delimitam uma região de área . Vamos ver o seu gráfico?
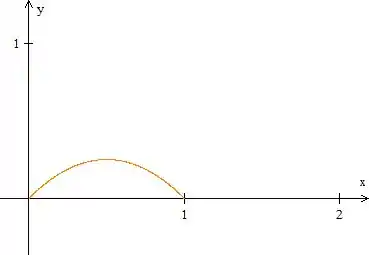
Queremos achar a equação de uma reta que passa pela origem.
Uma reta vai ser
Se ela passa na origem , então
No fundo, queremos calcular para que a área seja dividida pela metade
Passo 2
Vamos esboçar o que o enunciado nos diz:
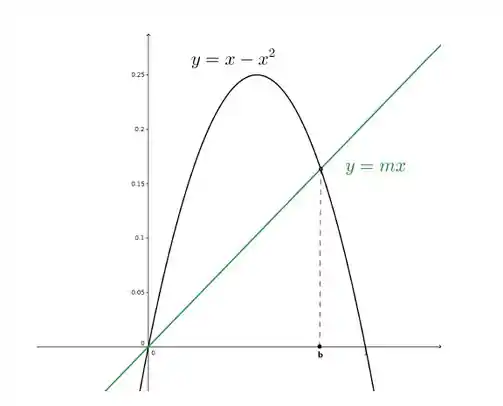
No desenho, foi desenhado uma reta genérica que corta .
OBS: Em problemas onde ainda não sabemos a equação de alguma curva, é muito útil esboçarmos uma situação genérica para essa curva e começar a fazer os cálculos a partir daí.
Igualando as equações, podemos achar os pontos de interseção:
Logo, .
Temos duas formas de prosseguir agora:
1. Dizendo que a área acima da reta é metade da área compreendida entre a parábola e o eixo .
2. Dizendo que a área acima da reta é igual a área abaixo dela.
Vamos seguir a forma 1, já que a área abaixo da reta é mais difícil de ser calculada (ou teríamos que integrar em relação a ou dividir em duas áreas).
Para isso é válido saber que a parábola intercepta em e .
Passo 3
Igualando a área acima da reta à metade da área abaixo da parábola, temos:
Assim, chegamos a uma equação para :
Logo, a equação da reta é: