Considere a região do primeiro quadrante limitada pelas curvas , e .
- Esboce a região .
- Calcule a área de .
Passo 1
Está bem, vamos começar com a letra . Como o problema falou que a região está no primeiro quadrante, vamos considerar só essa região. Começando com :
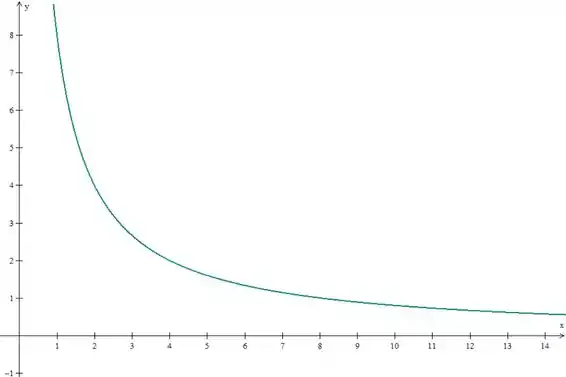
Agora, com , centrado na origem:
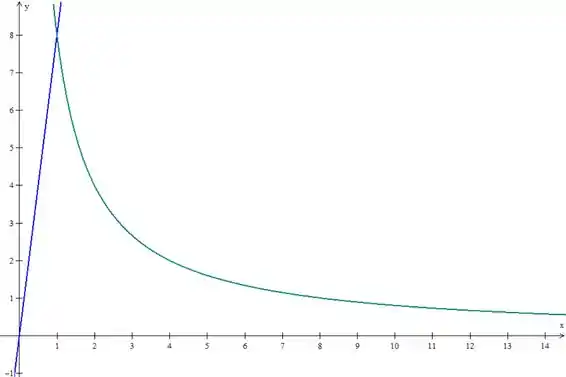
Finalmente, traçamos :
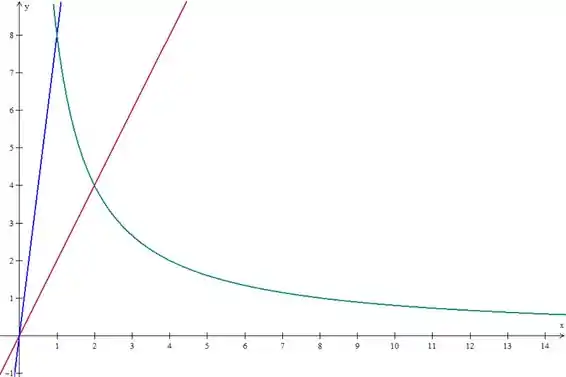
Veja que agora temos uma região fechada, ela será a região .
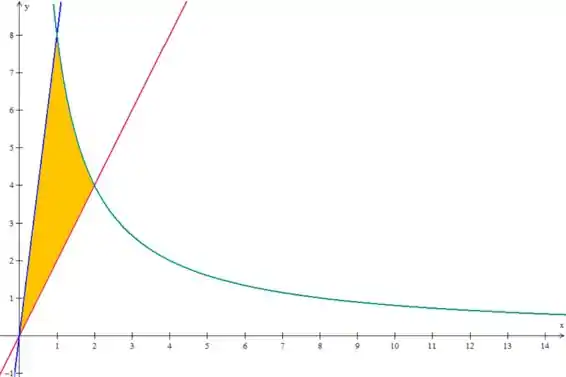
Passo 2
Agora vamos integrar a região , segundo a letra . De maneira geral, a área será:
Só que muda na região. Começa sendo a curva em azul, , e depois passa a ser , em verde. Assim, vamos separar nossa integral em duas:
Temos que tentar achar os intervalos de integração agora. O é a origem da região, que está em . Logo .
, como definimos na hora de separar a integral, é o ponto em que a curva superior muda, ou seja, na interseção entre e :
Agora, para , temos o ponto onde a região termina. Que ocorre na interseção entre e :
Pronto, já temos tudo que precisa.
Passo 3
Vamos integrar agora:
Para a primeira integral:
Para a segunda:
Então são: