Considere a função dada por
- Determine os intervalos de crescimento e decrescimento de
- Determine os intervalos onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.
- Faça um esboço do gráfico de indicando explicitamente as abscissas dos pontos de máximo, de mínimo e de inflexão.
- Sejam e as duas raízes da função no intervalo , , calcule
Passo 1
Vambora começar essa questão então! Como a primeira coisa que a questão pede são intervalos de crescimento e decrescimento, e a primeira derivada de uma função nos dá a inclinação da reta tangente, vamos derivar então:
Pela regra do produto:
Se a primeira derivada é negativa, a função decresce. Se positiva, a função cresce. Beleza, então pra gente ver em que ponto que o sinal começa a mudar, tempos que igualar à ! Vamos ter:
Oras, se essas funções são iguais, então
Olhando pro círculo trigonométrico:
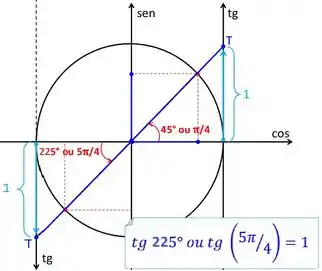
Então vamos ter:
Para
Para
Opa, mas peraí. O domínio da função não era ? Então valores de , que dão valores de maiores que , não rolam! Sendo assim, os pontos em que a primeira derivada zera são só:
Vamos ver então o que acontece com a primeira derivada em intervalos contendo esses pontos, mas dentro do domínio. Esses intervalos vão ser:
Pro primeiro intervalo, vamos escolher . Vamos ter então:
Pro segundo intervalo, vamos escolher . Vamos ter então:
E por fim, pro último intervalo, vamos escolher, por exemplo, . Vamos ter:
Então fechamos essa parte! Os intervalos de crescimento e decrescimento vão ser:
Passo 2
Show, vamos falar agora das concavidades! A análise é quaaaase a mesma. A diferença é que agora vamos precisar da segunda derivada. Então partiu:
Veja que é a própria , e logo:
E pela regra do produto:
E por fim, simplificamos para:
Se a segunda derivada for positiva, a concavidade é pra cima. Se negativa, a concavidade é pra baixo. Beleza, então pra gente ver em que ponto que o sinal começa a mudar, tempos que igualar à ! Vamos ter:
O que só é possível se:
E como o domínio é , estão valendo os valores pra em! As raízes da segunda derivada vão ser então:
Os intervalos que contem esses pontos e o domínio são então:
Pro primeiro intervalo, vamos escolher . Vamos ter então:
Pro segundo intervalo, vamos escolher . Vamos ter então:
Fechamos mais uma letra da questão em! A concavidade vai ser então:
Passo 3
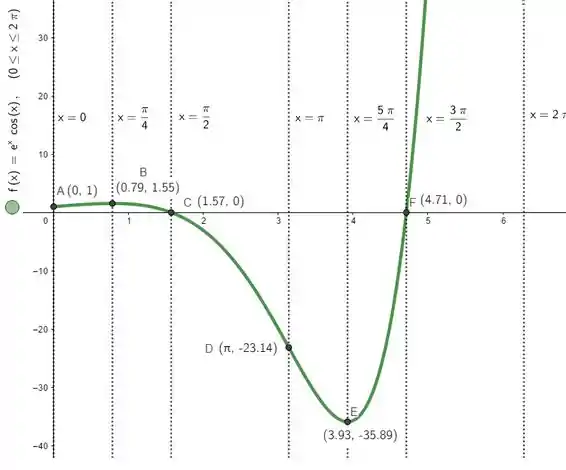
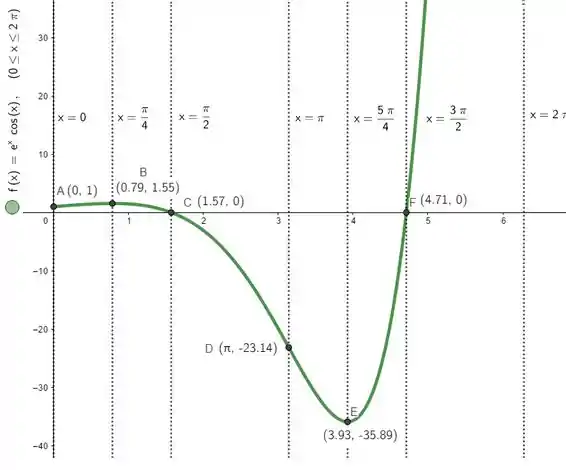
Bora esboçar esse gráfico então. Já temos intervalos que nos falam da concavidade e do crescimento/decrescimento. Só pra completar então, vamos ver interseções com os eixos! Se:
Então, se , teremos:
Ou seja, o ponto é um ponto da curva. Agora, seja , teremos:
O que só é possível se:
Que, pelo círculo trigonométrico, só ocorre se:
Beleza, mas como o domínio da função é da função, não é qualquer que pode não, e sim só os valores e ! Então vamos ter:
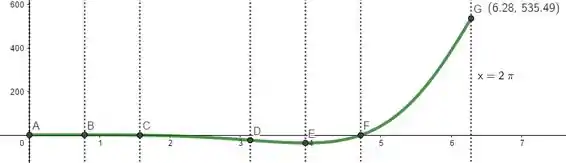
Prontinho, achamos os últimos pontos de interseção com os eixos, que vão ser e . Juntando essas informações com as do passo e , esboçamos:
Passo 4
A última questão pede pra gente calcular uma integral:
Onde são as raízes de . Como a gente viu elas na hora de esboçar o gráfico, é só por a mão na massa agora em! Vamos ter:
Vamos fazer a integral indefinida primeiro. E cara, dá uma olhada na função:
Uma exponencial vezes uma trigonométrica? Isso ai tem cheiro de resolução por integração por partes. Quer ver? Seja:
A integração por partes:
E logo:
Ok, não adiantou muita coisa por enquanto, porque caímos em outra integral de uma exponencial vezes uma função trigonométrica. Bem, vamos tentar integrar por partes de novo então. Veja só:
A integração por partes:
Fica:
Agora sim vai dar certo, quer ver? Juntando os dois resultados, temos:
E aplicando os limites de integração, temos: