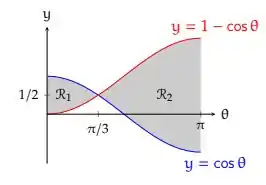
Considere a região do plano limitada pelas curvas e , com
Esboce a região , destacando os pontos notáveis da mesma.
(Atenção: não precisa determinar detalhadamente o crescimento/decrescimento nem a concavidade das funções envolvidas.)
Calcule a área de
Passo 1
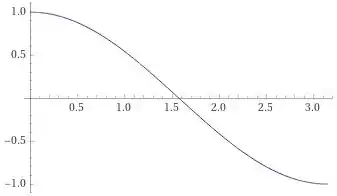
Bom pessoal, aqui na letra a) queremos esboçar a região que é definida por duas funções. Para isso, precisamos saber esboçar essas funções. A começar pela função , que o seu gráfico para é dado como:
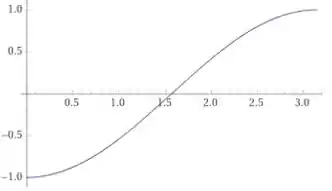
O segundo gráfico é o da função , o primeiro passo que podemos tomar aqui é realizar uma rotação ao redor do eixo para termos a função , que tem o seguinte esboço:
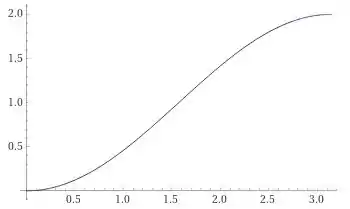
E translada-lo uma unidade para cima, para assim termos
Agora é só juntar os dois gráficos em um só e ver no que vai dar:
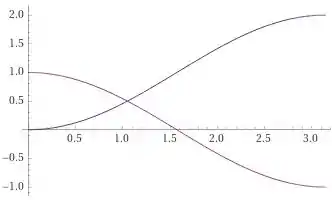
Perceba portanto que temos duas regiões aqui, uma onde e outra onde
Um ponto de interesse no nosso esboço de cima, é o ponto aonde as funções se cruzam, isso é, o ponto onde
Vamos resolver essa equação para encontra-lo:
Portanto, o ângulo é aquele cujo cosseno vale
E o valor das funções nesse ponto é e
Passo 2
Bom, agora que chegou o cálculo de verdade, né. Vamos calcular a área dessa região entre as funções, primeiramente vou dividir essa região em 2, pois uma parte temos uma função maior que a outra e depois isso inverte, por conta disso, vou dividir a região em 2, dessa forma aqui:
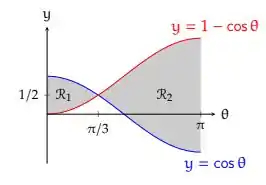
Dessa forma teremos que:
Vamos começar calculando a área da região 1.
Nesse caso , portanto o termo que teremos dentro da integral será e essa integral vai de até .
Podemos abrir essa integral na soma de duas integrais e retirar as constantes para fora da integral:
Por fim, ficaremos com:
Substituindo os limites...
Show de bolê, agora só falta a região 2
Passo 3
Na região 2, o que vai ocorrer é que é maior que , portanto teremos dentro da nossa integral e o intervalo de integração será de até . Bora lá
Podemos abrir essa integral na soma de duas integrais e retirar as constantes para fora da integral:
Cuja solução é:
Substituindo os limites,
Passo 4
Agora é somar a área das duas regiões!
Resposta