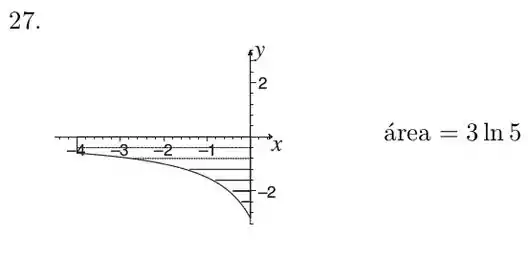
Esboce e encontre a área da região delimitada pelo gráfico de , pela reta e pelos eixos e .
Passo 1
Vamos esboçar o gráfico dessa função
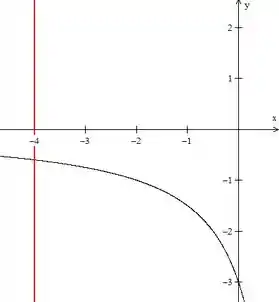
Como queremos a área entre a reta e os eixos e . Vamos trabalhar com o intervalo entre e .
Passo 2
Perceba que esta área está abaixo do eixo . Nesses casos sabemos que
Logo,
Passo 3
Integrando, ficamos com
Prontinho, resolvida nossa área!
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x