UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Integrais, Questão 2.5
2.5. Calcule o valor da menor área limitada entre as curvas e com .
Passo 1
Suave na nave?! Tá complicada essa questão? Relaxa que a gente vai te ajudar!
Nesse problema queremos obter a menor área possível entre as curvas e com pertencente ao intervalo .
E aí, como fazemos isso? 😐
Para obter essa área, podemos calcular a integral dessa região através de uma integral dupla.
Primeiramente, podemos esboçar a região que vamos obter e aplicar as variáveis nos limites de integração.
Para calcular a área, a função de integração deve ser .
Bora ver como é na prática? 😉
Passo 2
Podemos imaginar que a menor área que é formada entre e é dada no intervalo de entre e o primeiro ponto em que as curvas se encontram.
Como sabemos, as funções e são funções periódicas, então elas se cruzam infinitas vezes, porém em períodos definidos.
Para obter qual é esse valor de , temos
Como ...
Qual o ângulo cuja tangente é ? , não é? Veja só
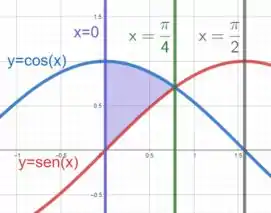
Entendeu essa parte? 😉
Passo 3
Perceba que a região é limitada superiormente por e inferiormente por , já varia de a .
Montando nossa integral, temos
Integrando com relação a
Integrando o resultado em função de pelo teorema fundamental do cálculo...
O que achou? Foi de boa? Responde aí! 😊
