Calcule a área da região limitada pela curva de equação e por sua assíntota, situada À direita do eixo .
Passo 1
Pra montar uma integral que sirva pra calcular essa área, precisamos entender a região . E para isso, vamos começar isolando na equação da curva:
Passo 2
Ok, então a região é limitada pelas curvas e e pela tal assíntota.
Essa assíntota está à direita do eixo , então, pra isso fazer sentido, é uma assíntota vertical. Não dá pra uma assíntota horizontal (ou oblíqua) ficar totalmente à direita de um eixo vertical, né?
E na expressão das nossas curvas temos o termo no denominador. Então quando , o denominador se anula. Além disso:
Então é a famosa assíntota que procuramos
Passo 3
Repare que as curvas e se encontram na origem. Então a região fica entre e .
Também vamos aproveitar que as duas curvas têm a mesma expressão, mudando apenas o sinal. Isso significa que mesmo sem conhecer a cara das curvas, sabemos que elas são espelhadas em relação ao eixo .
Passo 4
Resumindo:
- A região fica entre (ponto de encontro das curvas) e (assíntota vertical)
- As curvas são espelhadas em relação a origem
Nessa hora você vai lá no canto da folha e faz um esboço rápido pra ilustrar isso tudo. Seu esboço deve dar algo parecido com isso:
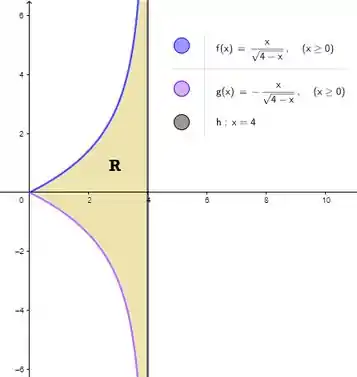
E graças ao nosso esboço, somos capazes de ver que a área de é igual a:
Passo 5
Agora basta calcular a integral! Vamos começar pela integral indefinida:
Fazendo , temos que e logo:
Voltando pra variável , isso dá:
Passo 6
Lembrando que a área é igual a:
Por causa da descontinuidade na assíntota em , pra calcular a área de vamos ter que tomar o limite:
Calculando então:
O primeiro limite vamos ver que vai tudo pra , logo:
E o segundo como não depende de :
Por fim: