Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 691234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja R a região do primeiro quadrante limitada pelos eixos coordenados e por y = 1 - x 2 . Suponha que a reta y = d divida R em duas sub-regiões de mesma área. Então d vale:

  1. 1 - 1 4 3
  2. 1 2 3
  3. 1 3 3
  4. 1 - 1 9 3
  5. 1 2

Passo 1

Vamos começar esboçando essa região R :

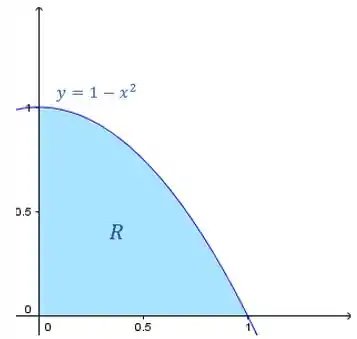
Passo 2

Acrescentando a reta y = d , que divide R em duas sub-regiões de mesma área A :

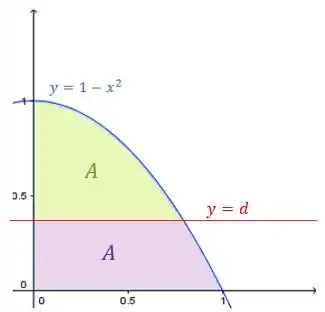
Passo 3

Então vamos calcular essa área A . A forma mais inteligente de fazer isso vai ser integrando em relação a y . Mas pra isso temos que escrever a curva y = 1 - x 2 como função de y :

y = 1 - x 2

x 2 = 1 - y

x = ± 1 - y

Como x > 0 na região R , temos:

x = 1 - y

Portanto, temos:

A = ∫ 0 d 1 - y d y = ∫ d 1 1 - y d y

Passo 4

Pra integrar isso aí fazemos a substituição simples:

u = 1 - y → d u = - d y

Assim, a integral indefinida fica:

∫ 1 - y d y = - ∫ u d u = - 2 3 u 3 2 + C

→ ∫ 1 - y d y = - 2 3 1 - y 3 2 + C

Passo 5

Usando a equação que achamos antes:

∫ 0 d 1 - y d y = ∫ d 1 1 - y d y

Vamos ter:

- 2 3 1 - y 3 2 0 d = - 2 3 1 - y 3 2 d 1

Esse - 2 3 já podemos cortar:

1 - y 3 2 0 d = 1 - y 3 2 d 1

Desenvolvendo:

1 - d 3 2 - 1 - 0 3 2 = 1 - 1 3 2 - 1 - d 3 2

1 - d 3 2 - 1 = 0 - 1 - d 3 2

2 1 - d 3 2 = 1

1 - d 3 2 = 1 2

1 - d = 1 2 2 3

d = 1 - 1 2 2 3

Passo 6

Temos que

2 2 3 = 2 2 1 3 = 4 3

Ou seja:

d = 1 - 1 4 3

Resposta

Letra (a)

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x