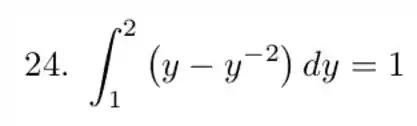Passo 1
Precisamos calcular a área entre as curvas. Não precisamos esboçar a curva, mas ajuda bastante a visualizarmos o nosso problema. Essas são nossas curvas
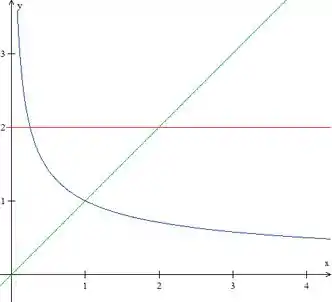
Passo 2
Precisamos encontrar os pontos de intersecção entre as curvas, para encontrar nossos limites de integração.
O outro limite já temos pela curva
Passo 3
Agora precisamos montar nossa integral e fazer a integração
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x