UFSC – Cálculo 1 – Lista 4.3 – Questão 5b
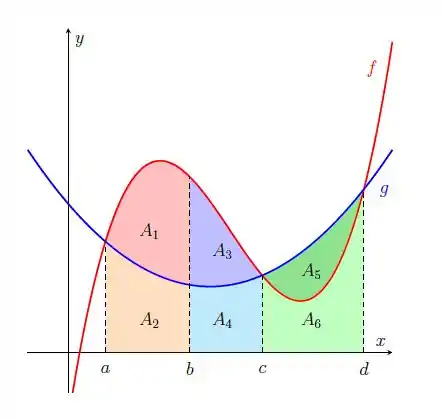
- Escreva as áreas e em termos de integrais
Passo 1
E aí pessoal, tudo bem?
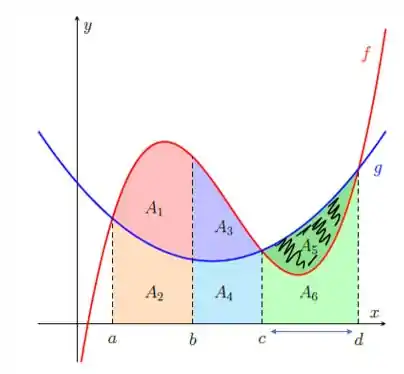
Essa questão parece complicada, mas vou ajudar você aqui! Temos o gráfico de duas funções. E temos indicações de regiões abaixo dessas regiões.
O problema pediu para escrever as áreas e em termos de integrais. Bom, então precisamos analisar o gráfico para cada uma dessas áreas e escrever como a integral de uma dessas funções.
Mas uma dica: caso a área esteja compreendida entre duas funções, a integral que representa essa área é a diferença entre elas! Dá uma olhada nesse gráfico genérico:
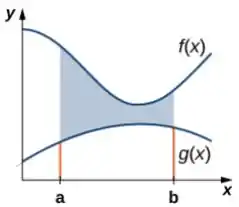
Se quiséssemos a área da , seria a partir dela, até o eixo . Mesma coisa se quiséssemos a área da . Mas o que nos interessa aqui é o que está entre: aí é só fazer a área da de cima MENOS a área da de baixo!
Mas calma, vou fazer passo a passo com você!
Passo 2
Vamos começar calculando a área :
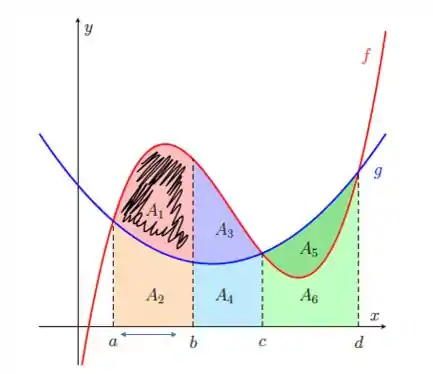
A área está compreendida no intervalo fechado . A função que está mais acima é a e a que está embaixo é a . Então a área entre elas é a diferença:
Tranquilo?
Passo 3
Agora vamos encontrar a integral da área :
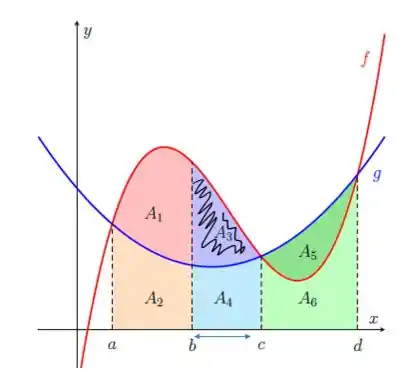
A área está compreendida no intervalo fechado . A função que está mais acima é a e a que está embaixo é a . Então a área entre elas é a diferença:
Passo 4
Vamos escrever a integral que representa a área . E agora ATENÇÃO
Nesse último intervalo as funções INVERTEM as posições! A função mais acima é a e a que está por baixo é a . E isso vai se refletir na integral que representa a área :
Então a área entre elas é a diferença, mas agora quem está por cima é a :
Beleza? E é isso!
Espero ter ajudado! Vamos para a próxima?