Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 191234567891011121314151617182021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre curvas

Considere os pontos 3,1 e 5,3

  1. Determine a equação da reta que passa por estes dois pontos
  2. Determine a equação da parábola x = - y 2 + b y + c que também passa por estes dois pontos.
  3. Determine a área da região delimitada pela reta e pela parábola acima.

Passo 1

a )

Vamos começar achando a reta, para isso só precisamos fazer

y - 1 x - 3 = 3 - 1 5 - 3

y - 1 x - 3 = 2 2

y - 1 x - 3 = 1

y - 1 = x - 3

y = x - 3 + 1

y = x - 2

Passo 2

b )

Aqui só precisamos substituir os valores do ponto na fórmula da parábola, x = - y 2 + b y + c

Substituindo 3,1

3 = - 1 2 + b . 1 + c

3 = - 1 + b + c

b + c = 3 + 1

b + c = 4

Substituindo 5,3

5 = - 3 2 + b . 3 + c

5 = - 9 + 3 b + c

3 b + c = 5 + 9

3 b + c = 14

Encontramos o sistema

b + c = 4 3 b + c = 14

Subtraindo a segunda equação da primeira vamos ter

3 b - b = 14 - 4

2 b = 10

b = 5

Voltando na primeira equação

5 + c = 4

c = 4 - 5

c = - 1

A equação da parábola vai ser

x = - y 2 + 5 y - 1

Passo 3

c )

Vamos começar fazendo a figura da parábola e da reta.

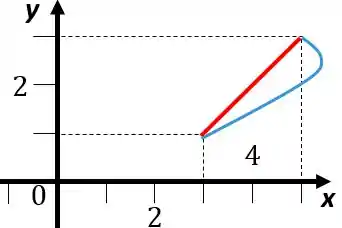
A parábola fica assim porque o coeficiente de y 2 é negativo, e a parábola tem o eixo de simetria paralela ao eixo x por ser x igual a alguma coisa de y .

Para achar a área vamos integrar ao longo de y ,, vamos ter

A = ∫ 1 3 f d i r e i t a - f e s q u e r d a d y

A função da direita é a parábola e a função da esquerda é a reta, precisamos escrever a reta em função de y

y = x - 2

x = y + 2

A área vai ficar

A = ∫ 1 3 - y 2 + 5 y - 1 - y + 2 d y = ∫ 1 3 - y 2 + 5 y - 1 - y - 2 d y =

⇒ ∫ 1 3 - y 2 + 4 y - 3 d y = - y 3 3 + 4 y 2 2 - 3 y y = 1 3 =

⇒ - 3 3 3 + 4 . 3 2 2 - 3.3 - - 1 3 3 + 4 . 1 2 2 - 3.1 = - 9 + 18 - 9 - - 1 3 + 2 - 3

⇒ 0 - - 1 3 - 1 = - - 4 3 = 4 3

Resposta

  1. y = x - 2
  2. x = - y 2 + 5 y - 1
  3. A = 4 3

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x