Considere a função
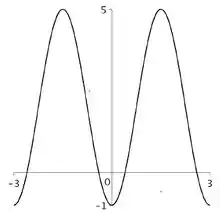
- Sabendo que a curva acima é o gráfico de , determine
- Determine todos os valores de que satisfazem a equação
- Calcule a área da região
Passo 1
Vambora começar essa questão então! A questão nos da , mas não ela inteira: falta achar . Pô, só precisamos então ver informações do gráfico pra achar essas constantes. Dá uma olhada nessa propriedade do cosseno:
Beleza, vamos usar ela, mas antes, vamos dar uma olhada num gráfico de uma função cosseno típica:
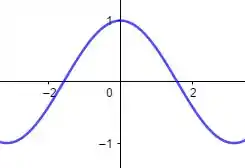
Opa! A partir de a função decresce, e a nossa cresce! Sendo assim, em :
O fator que multiplica só pode ser negativo! Portanto, . Beleza, vamos voltar então pra aquela propriedade do cosseno.
Multiplicando os dois lados por, temos:
Como , vamos ter que . Então pra não confundirmos, vamos trocar e de lado:
Somando nos dois lados:
E veja bem o gráfico:
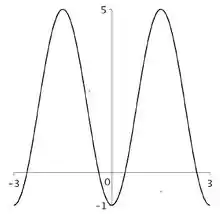
A função está limitada por e ! Logo se ambos são verdade:
Então temos:
Somando as duas equações, temos:
E logo:
Show. Nossa função, por enquanto, tá assim ó:
Falta agora só achar o . Pra isso, vamos dar uma olhada no círculo trigonométrico:
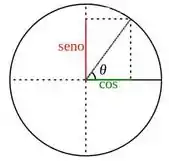
Vendo ele com calma, a gente percebe que acontece quando
Ok, mas e dai? Bem, da uma olhada na nossa função e seu gráfico:
Do gráfico do enunciado, temos que:
O que só é possível se:
Opa, mas já sabemos em quais arcos o cosseno dá ! São os arcos e (quaisquer outros arcos são côngruos). Sendo assim:
E igualamos o interior dos cossenos:
Show, encontramos ! Ele vai ser:
A função enfim ficará:
Passo 2
A próxima letra pede pra determinar todos os valores de que satisfazem a equação . Agora que temos a completa, fica mais tranquilo. Vamos ter:
Multiplicando os dois lados por
Fazendo a função trigonométrica inversa:
Falta agora a gente ver qual arco tem cosseno . Orá, um deles é o arco de ou em radianos. O outro é o arco de ou em radianos. Mas bem, a função cosseno é uma função oscilatória, certo? Então vamos de novo olhar o círculo trigonométrico:
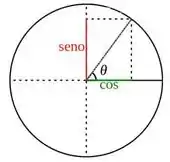
Olhando com cuidado, vemos que:
Sendo assim, temos:
E temos também:
Mas pera, não dá pra responder assim né? Até porque pra alguns valores de , não vai estar contido no intervalo do enunciado. Beleza, vamos testar alguns . Para :
Para :
E a gente para aí, porque e o achado está fora do intervalo. Pro outro arco, fazendo :
Pra :
E de novo paramos por aí porque . Fechamos a letra então! Os únicos valores de que satisfazem a equação são e
Passo 3
Última parte da questão: cálculo de área! Vamos ter a região:
Do gráfico da curva:
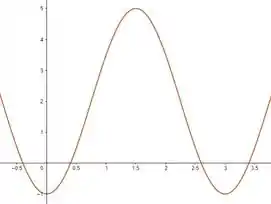
Vamos primeiro limitar em , beleza? Só pode . Logo:
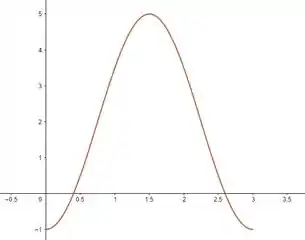
Agora vamos limitar em . Como está entre um valor e a própria curva, vamos ter a região :
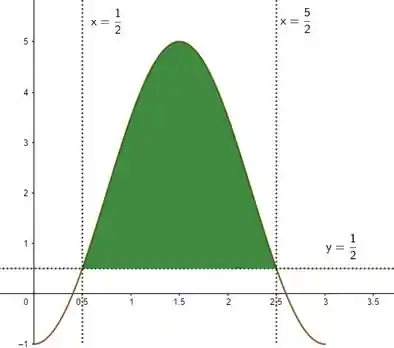
Perceba que na letra a gente já achou os pontos em que e se interceptam! Bem, agora que sabemos a cara de , precisamos calcular a área! E qual a melhor forma de fazer isso se não integrar?
Um porém, essa integral não pode ser direta, porque dá uma olhada em como ficaria se fizéssemos:
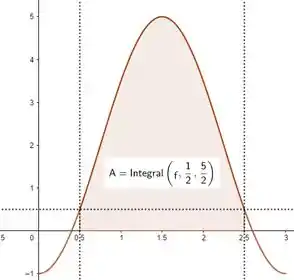
Ta vendo que tem um retangulozinho ali em baixo que a integral acaba contando? Temos que descontar a ��rea desse retângulo em! Então, primeiro, calculando a área pela integral:
Agora calculando a área do retângulo:
E calculando a área total:
Temos: