USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 2, Questão 3.3
Determine para que a área delimitada por e a reta seja igual a .
Passo 1
Eaee!!! Belezinha? Bom... queremos calcular para que a área delimitada por e a reta seja igual a .
Muita informação, né? Então vamos com calma...
Queremos descobrir a seguinte área:
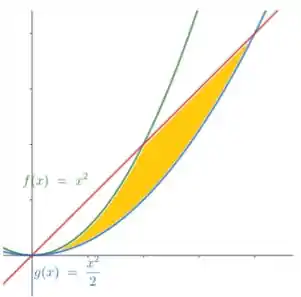
Onde a reta vermelha é uma reta qualquer .
Para descobrirmos essa área, temos que calcular as interseções das curvas e a reta .
E aí? Bora lá?
😉
Passo 2
Então... vamos descobrir primeiramente o ponto de interseção entre a curva e a reta . Para isso, devemos igualar as duas equações:
Agora, entre a curva e a reta :
Com isso, podemos observar o seguinte gráfico:
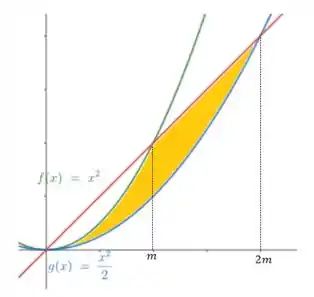
Com isso, agora podemos calcular nossa área e descobrir o valor de !!
Passo 3
Analisando a figura acima, vemos que a nossa área em amarelo é dada por:
No enunciado, vemos que .
Dessa forma, substituindo na expressão e desenvolvendo, temos:
Entendeu direitinho? Responde aee ;)
