UFSCAR – Cálculo 1 – P3 – Questão 4
Esboce a região e encontre sua área (se for finita)
Passo 1
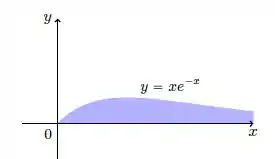
Oi pessoal, tudo bem? O problema nos pediu para calcularmos essa área aqui
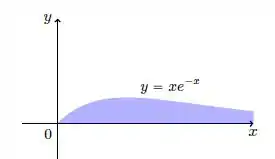
Com
A região hachurada está acima do eixo e abaixo da curva
E o ? Vai de até Até quanto? Até mais infinito!
E essa área pode ser calculada se essa integral foi convergente, ou seja, se o cálculo dessa integral com o limite superior sendo resulta em um número! Essa integral nós chamamos de integral imprópria
A ideia então é resolver usando o método mais apropriado! Mas relaxa, vou fazer com você!
Passo 2
Precisamos resolver essa integral
Então antes de mais nada, precisamos trocar essa integral imprópria, por limites apropriados
Como temos uma função algébrica multiplicada por uma exponencial vamos usar a integração por partes.
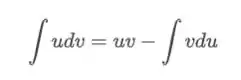Lembrando que o método por partes é assim
Agora vamos substituir:
Agora vamos substituir nos limites:
Tudo bem até aqui?
Então agora nossa missão é: avaliar o limite do resultado quando
Passo 3
Vamos começar recapitulando! Tínhamos que resolver essa integral
E achamos
Agora basta fazermos o limite quando do resultado da integral
Como o limite da soma é a soma dos limites podemos avaliar os termos separadamente
Aplicando a regra de L’Hopital no primeiro, temos o seguinte
Assim nosso limite fica
Olha só! Encontramos um resultado finito! Isso significa que a integral imprópria converge é a área embaixo da curva é
Agora sim! Terminamos!
Espero ter ajudado!
=D