4) Considere a região do plano limitada pelas curvas e com
- Faça um esboço das curvas envolvidas no problema, indicando os pontos notáveis e hachurando a região .
- Calcule a área da região .
Passo 1
Bora lá, questão de esboço de gráfico e área entre curvas. Como temos duas curvas:
Um bom primeiro passo é ver quando elas se encontram. Igualando elas então, temos:
O que acontece em e em . Logos os pontos de interseção são:
Beleza, achamos dois pontos interessantes. Mas tem mais pontos que podemos achar pra auxiliar nosso esboço. Por exemplo, os pontos das raízes da parábola . Vamos ter:
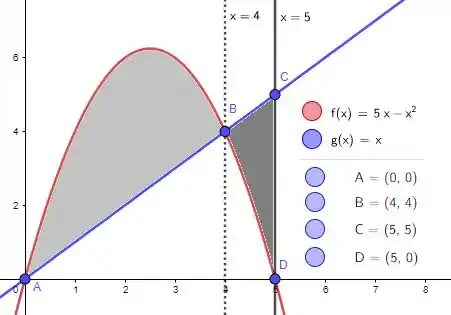
As raízes são então e , logo temos a origem de novo e o ponto , que se localiza exatamente na limitação imposta pelo enunciado. Pra fechar, adicionamos então o ponto que faz parte da reta e está localizado no limite superior do intervalo. Sendo a parábola uma parábola de concavidade pra baixo, uma vez que o termo ao quadrado está negativo, usamos esses pontos para esboçar a região :
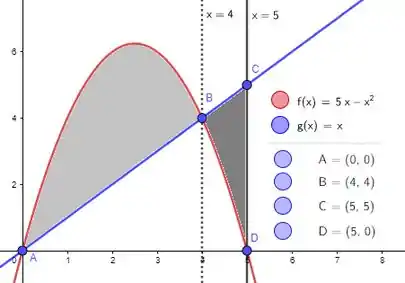
Que no caso será tanto a área cinza escura quanto a área cinza claro . Ou seja:
Vamos calcular um de cada vez então.
Passo 2
Começando pela área cinza clara. Dá uma boa olhada nela:
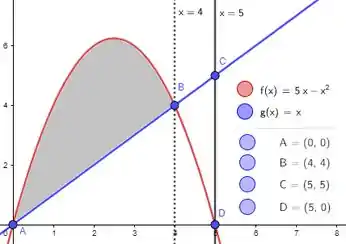
Oras, o que é essa área se não a área roxa :
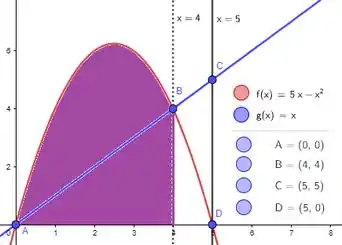
Menos a área verde :
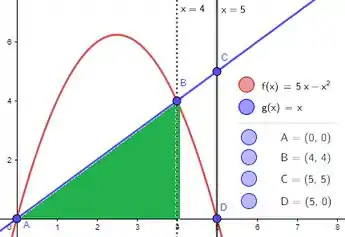
E as áreas roxas e verdes são bem diretas de calcular porque são áreas abaixo das funções que conhecemos! Vamos ter então:
Passo 3
Agora vamos ver a área cinza escura:
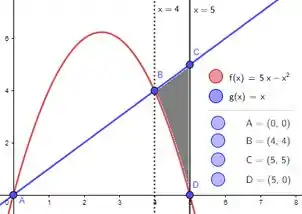
Ela é bem parecida com a cinza clara né? A diferença é que quem está por cima agora é a reta e não a parábola! Sendo assim podemos entender essa área como a área bege menos a área azul :
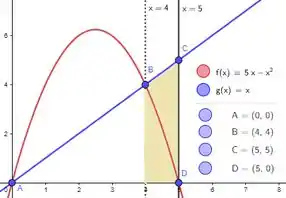
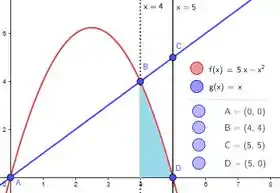
E logo:
Passo 4
Agora é só juntar. Seja:
A área da região vai ser então: