UFSC, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFSC - Lista 2.1 - Áreas entre curvas, Questão C1
Mostre que a área do círculo de raio é .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente mostrar que a área do círculo é igual a . Pra isso, vamos usar a equação da circunferência de raio , , que isolando o fica:
Se a gente pegar só a raiz positiva e integrar entre os limites horizontais do círculo, que é e , vamos ter a semicircunferência:
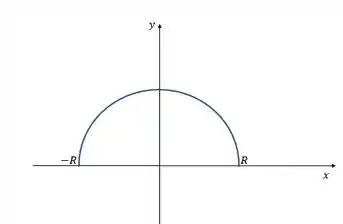
Multiplicando por pra pegar a região de cima e de baixo do círculo, vamos ter a área total que é dada pela integral:
Pra resolver essa integral e facilitar nossas contas, podemos usar uma substituição trigonométrica, fazendo , de modo que:
Então, substituindo isso na fórmula de área, vamos calcular a integral:
Vamos lá!
Passo 2
Vamos elevar os termos do radicando ao quadrado:
Colocando em evidência:
Usando a identidade trigonométrica , temos:
Tirando a raiz:
Multiplicando os termos:
Agora vamos usar outra identidade trigonométrica, fazendo :
Integrando, temos:
Aplicando os limites de integração:
Como , temos:
Logo, simplificando:
Como queríamos demonstrar.
Valeu, galera! Até a próxima! 😉