Calcule a área da região compreendida entre o gráfico de
E o eixo , com
Passo 1
Po o primeiro passo é sempre tentar ver onde a curva está acima do eixo e onde está abaixo! O legal é tentar esboçar o gráfico. Aqui é um pouco complicado fazer isso, mas sabemos que essa função só se anula onde o numerador for 0, ou seja, .
Agora segue aqui comigo:
Então se for negativo, . Agora se for positivo, então . Então a gente pode pensar em algo assim:
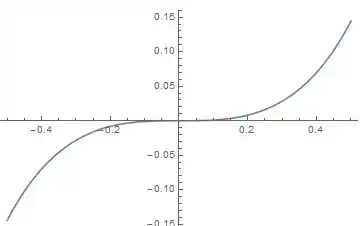
Repara que o denominador não pode zerar, e nele também temos uma raíz quadrada. Então a função não existe para . Porém como nosso limite de integração superior é , não vamos nos preocupar com isso.
Passo 2
Legal! Estamos vendo que a nossa área está acima do eixo , então vamos usar a seguinte fórmula:
Passo 3
Agora temos que resolver essa integral aí em cima. Essa integral sai por substituição trigonométrica, concorda? Vamos resolver a primitiva, voltar para e aplicar os limites de integração:
Bem, esse é o caso , .
Temos que fazer,
Substituindo na integral dada.
Passo 4
Agora, usando a substituição
Então a integral fica assim,
Voltando para :
Passo 5
Usando o triângulo retângulo para converter o na variável inicial:
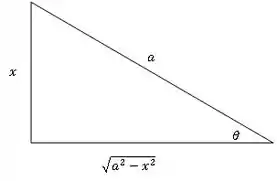
Então temos que
Passo 6
Agora vamos aplicar os limites de integração:
O que vai dar: