Considere as funções e . Calcule a área da região limitada pelos gráficos de e no intervalo .
Passo 1
A gente sempre começa esse tipo de questão tentando entender a disposição gráfica das funções. Na prática, eu até sei como fica o , mas não sei como é o desenho do . A questão é saber dentro da região quem fica por cima e quem fica por baixo, para armar a integral da área corretamente, dessa maneira não precisaríamos nem do desenho. Vamos procurar onde os gráficos se interceptam, ou seja, onde :
Descobrimos que os gráficos se tocam justamente nos limites do intervalo pedido no enunciado, em e . Dessa forma, para saber qual gráfico está por cima e qual gráfico está por baixo no intervalo dado basta substituir um ponto qualquer no intervalo e ver qual dos dois gráficos tem maior valor, sendo esse o que ficará por cima:
Assim, o gráfico superior é e o inferior é no intervalo dado, como na figura abaixo, onde o gráfico vermelho é e o azul é :
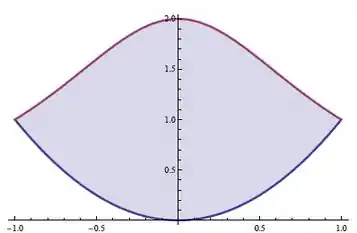
Passo 2
Pelas informações que chegamos, a área seria dada pela seguinte integral:
Vamos resolver agora! Um termo integrado por definição como polinômio e o outro como arco tangente: