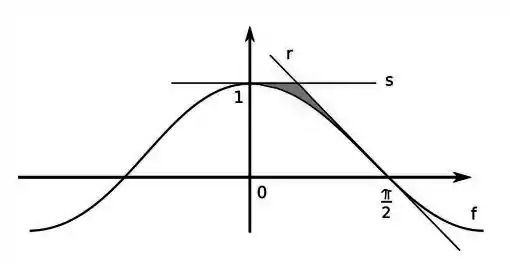
Na figura abaixo, sabendo que , a reta é a reta horizontal e a reta é tangente ao gráfico da em , ache a área da região cinza.
Passo 1
Podemos começar encontrando a equação da reta . Sabemos que ela é tangente à função em . Pela equação da reta tangente à função num ponto temos:
Temos que:
Sabemos também que:
Portanto:
Passo 2
Substituindo tudo:
Ou seja:
É a equação da reta .
Agora precisamos saber onde é o ponto de encontro entre e para montar nossa integral:
Igualando:
Ou seja, é o ponto:
Passo 3
Fazendo a integral, temos que a área é igual à:
Simplesmente pelo fato de subtrair a área do cosseno do limitante superior, que são as retas e . Calculando:
Plugando os limites de integração:
Obtemos, finalmente, que:
Passo 4
Substituindo tudo de volta, temos:
Arrumando: