UFSC, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFSC - Lista 2.1 - Áreas entre curvas, Questão P2f
Em cada item, determine a área da região delimitada pelos gráficos das curvas.
f) e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente determinar a área entre as curvas de e , que é essa região aqui em amarelo:
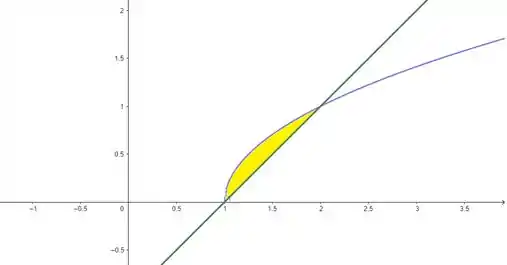
Repare que é mais interessante agora, “varrer” a região primeiro em relação a , porque ela é limitada horizontalmente por (curva em roxo) e (reta em verde). E aí ela passa a ser limitada verticalmente de a , onde as curvas se interceptam. Então, nossa integral de área tem a forma:
Onde, nesse caso, , e .
Vamos lá!
Passo 2
Montando nossa integral de área, temos:
Assim, integrando usando a regrinha da potência (), vamos ter:
Aplicando os limites de integração:
Simplificando, temos a nossa área:
Valeu, galera! Até a próxima! 😉