Área entre Curvas
Calcule a área da região limitada pelos gráficos de e no intervalo
Passo 1
Vamos começar desenhando essa área. O gráfico azul é o e o vermelho é :
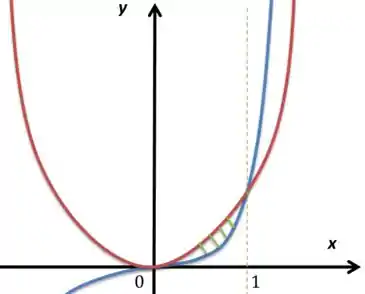
Ok, a área que estamos procurando é essa pintada de verde aí, justamente entre as duas interseções entre os gráficos. A gente percebe que nesse espaço o é maior, então a integral será , isso nos limites já determinados de e :
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x