Área entre Curvas
Dado o gráfico de abaixo, determine a área compreendida entre os gráficos de e , para .
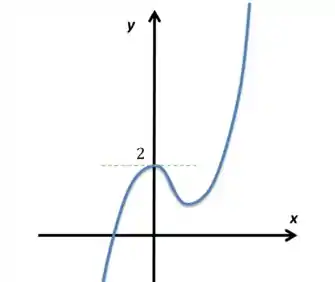
Passo 1
Para desenhar essa parábola no gráfico já dado e descobrir a área entre eles é interessante que achemos possíveis raízes e os pontos de interseção. Primeiro, falando de raízes, podemos analisar dessa maneira: se a parábola tem a boca virada para cima e descobrirmos que seu ponto de mínimo (derivando e igualando a ) tem positivo saberemos que ela não tem raiz, justo? Então vamos fazer isso:
Não existem raízes, então. A parábola é inteiramente positiva. Continuando, procuramos interseções agora, o que achamos igualando as funções, né?
Vamos desenhá-lo então, juntando todas essas informações:
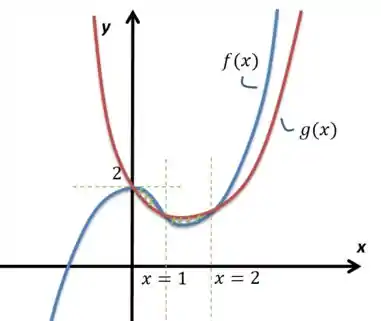
Repara, a área que procuramos é essa marcada em verde. Até temos azul por cima e apartir daí até o vermelho fica por cima. Armamos a integral, então: