Esboce a região delimitada pelas curvas e e calcule o valor numérico de sua área.
Passo 1
Essas curvas são tranquilas de esboçar:
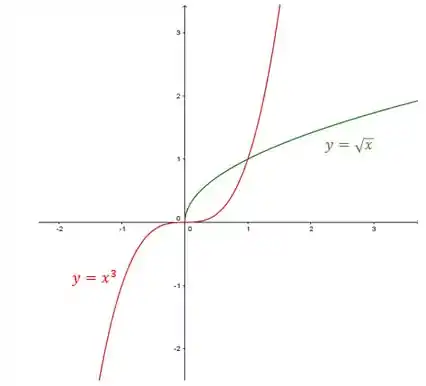
Então a região que ele pediu é a que está ali na meiúca entre as duas:
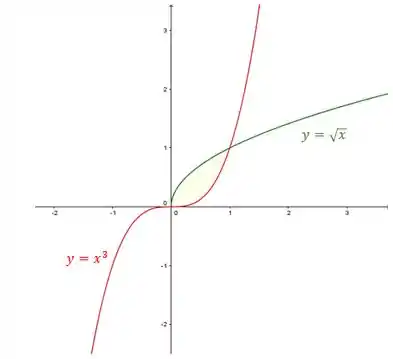
Olhando mais de perto:
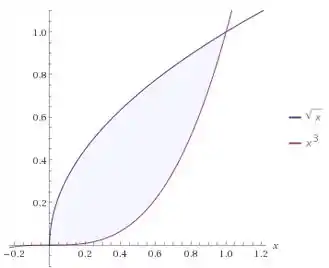
Passo 2
Pela figura podemos ver que as curvas se encontram em e , e, de fato:
E como a curva está sempre acima da curva , a integral que vai nos dar a área dessa região é:
Passo 3
Show, agora é só calcular a integral!
Pronto, aí está a área! :)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x