Origem do Exercício
Encontre a área da região sob a curva , no intervalo . Interprete geometricamente o resultado.
Passo 1
A área da região sob a curva é simplesmente a integral da função no intervalo que foi dado! Ou seja, precisamos calcular isso aqui:
Passo 2
Para resolver essa integral, vamos começar separando essa em outras três:
E todas essas integrais são de polinômios. De forma que a integral indefinida é:
E substituindo os limites de integração, achamos o seguinte:
Passo 3
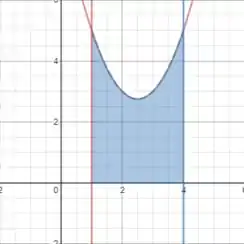
Como interpretação geométrica do problema, podemos esboçar a parábola dada pela função, e marcar a área que estamos integrando:
Resposta
A área da região sob a curva é
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x