Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 711234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697072737475767778798081828384858687888990919293949596979899100

Enunciado

2) Seja R a região plana delimitada pelas curvas y = cos ⁡ π x , y = sin ⁡ π x e y = 0 conforme o esboço abaixo:

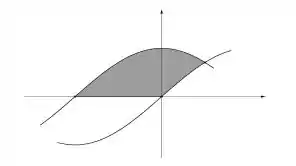
  1. Escreva a área da região R através de uma soma de integrais.
  2. Calcule a área da região R .

Passo 1

a )

Bem, antes de qualquer coisa, necessito que você saiba que o seno é sempre o cara que passa por y = 0 quando x = 0 . Logo...

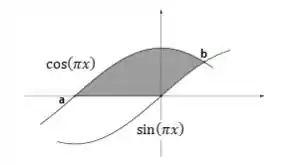
Bem, a área de uma região R de acordo com a fórmula é dada por...

A R = ∫ a b f x - g x d x

Onde o a ,   b é o intervalo de integração em x , f x é a função que está por cima e a g a que está por baixo.

No caso, o nosso problema aqui é encontrar quem são cada um desses caras ;)

Passo 2

Primeiro eu preciso que você note que teremos que dividir a integral em outras duas, pois em cima do eixo y ( x = 0 ), a função que está por baixo muda:

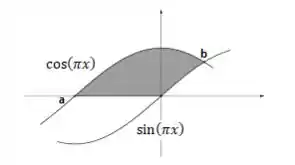
Antes do x = 0 , a função que está por baixo é o g x = 0 e depois do x = 0 ... g x = sin ⁡ π x ...

A R = ∫ a b f x - g x d x

A R = ∫ a 0 f x d x + ∫ 0 b f x - sin ⁡ π x d x

O f x , função que está por cima, em ambas integrais, ela é a curva do cosseno...

A R = ∫ a 0 cos ⁡ π x d x + ∫ 0 b cos ⁡ π x - sin ⁡ π x d x

Passo 3

Pois bem, ainda nos falta encontrar quem é o a e quem é o b dessa parada. Não se preocupe, pois novamente se olharmos à região...

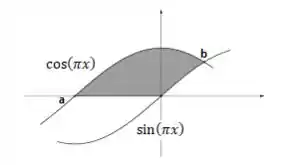
Vamos notar que o a é o ponto de encontro da função cosseno coma função y = 0 ...

cos ⁡ π x = 0         →

Isso só acontece se o ângulo for - 90 ° ...

π x = - π 2         →

a = x = - 1 2

Enquanto isso, o b é o encontro da função sino com a cosseno...

cos ⁡ π x = sin ⁡ π x

Essa igualdade acontece quando o ângulo é de 45 ° ...

π x = π 4       →

b = x = 1 4

Portanto...

A R = ∫ - 1 2 0 cos ⁡ π x d x + ∫ 0 1 4 cos ⁡ π x - sin ⁡ π x d x

Passo 4

b )

Aqui é só resolver o resultado dessas integrais...

A R = ∫ - 1 2 0 cos ⁡ π x d x + ∫ 0 1 4 cos ⁡ π x - sin ⁡ π x d x

Passo 5

Vamos começar pela primeira...

∫ - 1 2 0 cos ⁡ π x d x

Fazendo uma substituição simples...

π x = a     →         d a = π d x         →           d x = d a π

Trocando também os limites de integração...

x = - 1 2         →         a =   π - 1 2 = - π 2

x = 0         →         a =   π 0 = 0

∫ - 1 2 0 cos ⁡ π x d x = 1 π ∫ - π 2 0 cos ⁡ a d a =

1 π sin ⁡ 0 - sin ⁡ - π 2 = 1 π 0 + 1

= 1 π

Passo 6

Calculando agora a outra...

∫ 0 1 4 cos ⁡ π x - sin ⁡ π x d x =

sin ⁡ π x π + cos ⁡ π x π 0 1 4 =

sin ⁡ π 4 π + cos ⁡ π 4 π - sin ⁡ 0 π + cos ⁡ 0 π =

2 2 π + 2 2 π - 0 π + 1 π = 2 2 π + 2 2 π - 1 π =

2 π - 1 π

Então...

A R = ∫ - 1 2 0 cos ⁡ π x d x + ∫ 0 1 4 cos ⁡ π x - sin ⁡ π x d x   →

A R = 1 π + 2 π - 1 π = 2 π

Resposta

a )

A R = ∫ - 1 2 0 cos ⁡ π x d x + ∫ 0 1 4 cos ⁡ π x - sin ⁡ π x d x

b ) 2 π

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x