1) Calcule a área:
a) Da região .
Passo 1
Oiee galerinha, como vocês estão? Tudo belezinha por aí?

Quero todo mundo felizinho assim no fim dessa questão, show? Então vamos!!
Nesse exercício, precisamos calcular a área formada por essa informação dada pelo enunciado.
Apesar de parecer confusa, essa sentença toda do enunciado nos fala o seguinte:
A região está em um plano que pertence ao , ou seja, em um plano dos números reais tanto para o eixo quanto para o eixo . Dentro desse plano, as funções que definem as nossas áreas são e . Essas são as informações mais importantes até agora. Nossa área está definida nos valores de que são maiores ou iguais a na primeira função e nos valores de que são menores ou iguais a na segunda função.
Ou seja, temos que calcular uma área entre 2 curvas! Legal, mas como fazemos isso?
A área entre curvas é uma das principais utilizações das integrais, já que quando fazemos operações entre as curvas e integramos em um intervalo definido, encontramos a área formada entre elas. Ou seja:
Essas funções que apareceram ( e ) serão as nossas curvas em questão. Já o intervalo são os pontos onde as curvas coincidem. E o sinal que aparece antes de uma função na integral vai depender de se ela fica abaixo ou acima da área que queremos calcular.
Sabendo disso, precisamos descobrir onde essas duas funções assumem valores iguais, ou seja, onde as curvas se cruzam. E, então, teremos qual o intervalo da nossa integração.
Vamos calcular?
Passo 2
Como vimos no Passo 1, para encontrarmos o intervalo da nossa integração precisamos encontrar os pontos que as funções são iguais.
No nosso caso:
Como temos uma equação do segundo grau, precisamos encontrar as duas raízes. E elas serão:
Legal, definimos o intervalo de integração!
Passo 3
Antes de integrarmos, precisamos checar os gráficos das curvas para encontrarmos a melhor operação possível entre elas. Aqui definiremos se vamos somar ou subtrair as duas curvas na hora da integração.
Colocando as duas curvas em um gráfico vemos que:
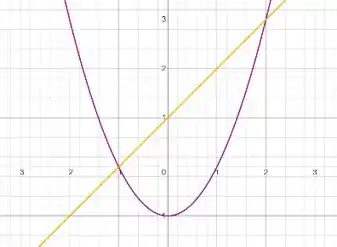
A linha laranja define e a linha roxa define . E a gente quer a região , que fica abaixo da reta laranja e acima da parábola roxa.
Vamos definir que:
A integral de uma curva é a área ABAIXO dessa curva no gráfico. Então fazemos a integral de porque a área que queremos está abaixo de . Mas a área abaixo de não faz parte da nossa região, então esse termo vai ser subtraído na integral. E a nossa integral fica assim:
Substituindo:
Aplicando a distributiva:
Passo 4
Agora que encontramos a integral, só resta calcularmos! Como temos soma entre os termos, podemos reescrever como:
Integrando:
Aplicando o intervalo:
Simplificando:
Encontramos a área!
Ufaaa! Terminamos a questão!

Bora lá resolver mais uma então?