1.3 Seja a região finita do plano, delimitada pelas curvas e . A área dessa região é representada pela expressão integral:
Passo 1
Olá, pessoal! Tudo bom? Nessa questão nós temos que encontrar a integral que representa uma área determinada por duas curvas.
Para montar essa integral, primeiro a gente vai precisar visualizar que a área é essa que quero integrar, identificandos os seus limites de integração.
Então para começar, vamos traçar as curvas dadas e encontrar essa região.
Bora lá!
Passo 2
A primeira função que o problema deu foi . E a função raiz quadrada tem essa cara aqui:
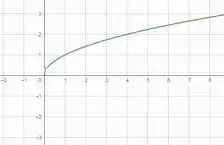
Já a função é uma reta!
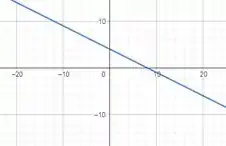
Juntando as duas ficamos com,
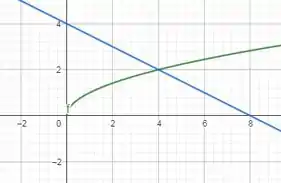
Agora precisamos saber onde as curvas se interceptam para calcular a área.
Passo 3
Para igualar as curvas, vamos isolar da segunda equação
Igualando a . Ficamos com
Agora vamos achar quanto equivale esse ponto em
Nossa região ficou assim,
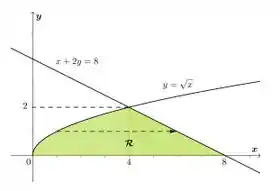
Bora montar a nossa integral?
Passo 4
Repara que a integração na variável será mais simples, pois identificamos mais fáceis os limites de integração (a região vai de até ).
Com isso, nossa integral é a área entre as curvas e no intervalo . Ficando a seguinte integral
Opaaa! A resposta correta é a letra D de dinossauro!
Resposta
Letra D