Área entre Curvas
Determine a área entre as curvas e , com .
Passo 1
A gente já sabe como é o gráfico de . Se considerarmos que é a inversa da função , dado ainda que os únicos pontos de encontro das figuras são e , o que descobrimos igualando as duas funções, a região que nos interessa é a seguinte:
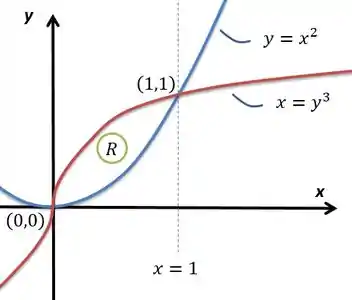
Esse é a região que nos interessa substituindo valores entre e vemos que é maior que nesse intervalo.
Passo 2
Dessa maneira, a integral de sua área será dada da seguinte maneira:
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x