Calcule a integral
onde é o pedaço dada curva dada pela equação , com , , orientada no sentido anti-horário. Justifique.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

A questão foi bem direta com a gente, apenas nos deu uma integral enorme e a região de integração .
A integral que foi dada é descrita por , onde
E e a região limitada pelas equações quando e .
E aí? Tem ideia do que fazer? 👀
Temos uma pista muito forte na construção da integral. Perceba que temos duas funções do tipo dentro da integral.
Esse é um indicio muito forte de que temos que usar o nosso querido Teorema de Green!
Mas pra usar esse teorema, temos que verificar se nossa região de integração é fechada.
Esboçando acurva e hachurando os intervalos onde e , vamos obter.
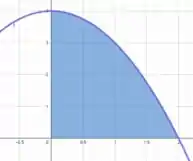
Com isso, podemos ver que nossa região é sim fechada! Então sinal verde pra aplicar o teorema! 😍
Preparado pra isso? Bora lá!
Passo 2
O Teorema de Green é dado seguindo a seguinte relação
Nossas funções e são enormes e dariam um grande trabalho integra-las.
Mas veja só com a aplicação do teorema!
Temos que calcular e primeiramente.
Como e , derivando com relação a , temos
Podemos dividir essa derivada em duas, veja só
Na primeira derivada, vamos usar o método de derivação polinomial.
Já na segunda derivada, vamos usar um misto entre a regra do produto e a regra da cadeia. Isso porque é um produto de funções e em um momento da regra do produto, vamos ter que calcular a derivada de e essa função é calculada pela regra do produto.
Veja só!
A regra da cadeia é dada pela derivada de dentro multiplicada pela derivada de fora, onde substituímos por
Voltando a
Logo, a derivada de com relação a é
Tranquilo até aqui? 😉
Passo 3
Agora vamos calcular a derivada de com relação a
Da mesma forma podemos dividir as derivadas
Na primeira derivada, vamos aplicar a regra da cadeia apenas e na segunda derivada vamos aplicar o mesmo misto entre a regra do produto e a regra da cadeia. Fazendo a mesma substituição por
Simplificando e substituindo por de volta
Agora na segunda derivada
Da outra derivada, já vimos que , então
Simplificando o resultado
Com isso a derivada de com relação a é
Bacana, não é? 😁
Passo 4
Voltando para a integral
Subtraindo os resultados de e , temos
Viu só? Da um pouquinho de trabalho para aplicar as derivadas, mas veja como nossa função de integração ficou bem mais simples.
Com isso, temos
Só nos resta descrever a região de integração como os limites de integração . Voltando para a figura que descreve nossa região
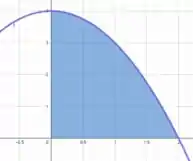
Podemos descrever nossa região pelo tipo com variando entre um intervalo numérico e entre um intervalo de duas funções.
Analisando a figura, vemos que varia entre e . Já varia entre e , logo nosso intervalo de integração será
Na integral vai ficar assim
Grande diferença, não é?
Passo 5
Calculando a integral de com relação a vemos que estamos integrando algo que se comporta como uma constante, então a integral de uma constante é a própria constante multiplicada pela variável de integração.
Aplicando os limites de integração
Agora com base nesse resultado integramos com relação a pelo método de derivação polinomial.
Aplicando os limites de integração, vamos ter
Logo a integral que tínhamos lá no início
Fala a verdade! Esse teorema é uma maravilha, não é? 😍
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
