Considere a região delimitada pela parábola , pela reta tangente a esta parábola em e pelas retas e .
Esboce a região , indicando claramente a região na sua figura.
Determine a equação da reta tangente à parábola em .
Encontre a área da região
Passo 1
É o seguinte, essa parábola não é muito difícil de fazer não, ela tem o vértice em e boca para cima. Acontece que para desenhar a região nós precisamos da reta tangente ao ponto da parábola. Até dá para fazer uma aproximação sem a equação (além de que ele só pede a equação da reta na letra ), mas prefiro calculá-la para a achar a região com precisão.
Sabemos que a reta tem coeficiente angular igual a , com e passa no ponto . Assim, modelando a reta por :
Assim, achamos a reta , reta decrescente que toca o eixo em . Vamos fazer o desenho com a reta e a parábola limitado pelos eixos e :
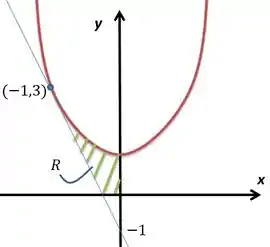
Passo 2
Como já achamos, a reta é
Passo 3
Podemos observar que a reta toca o eixo em
Ou seja, de até teremos que fazer uma integral de área que é a diferença entre os gráficos da parábola e da reta. Já no intervalo devemos integrar da parábola até o eixo, ou seja, a própria integral da parábola. Logo, nossa área pode ser calculada por: