Determine a área da região , onde:
é a região limitada pela curva , pelo eixo e pelas retas e .
Passo 1
Primeiro eu vou pegar essa função e abrir melhor com o em evidência:
Olha, o tem raiz em . Já o não tem nenhuma raiz e é sempre positivo. Ou seja, ao que parece essa função do terceiro grau só tem raiz em e é negativa quando é negativo e positiva quando ele é positivo. Essas informações já são suficientes para esboçar algo assim:
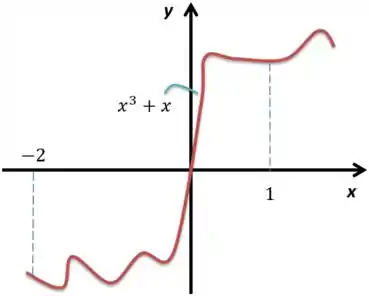
Passo 2
Olha lá uma parte em que está acima do eixo e outra que está abaixo. Então o que faremos? Vamos separar em duas regiões! A primeira está à esquerda do eixo e vamos chamar de e a segunda, que está a direita, vamos chamar de . Portanto,
Passo 3
Primeiro vamos analisar a área . Nessa área é menor que 0, então vamos fazer
Passo 4
Agora para a área aquela que está à direita do eixo , temos que a função é positiva. Então,
Passo 5
Agora a gente só precisa somar os dois resultados, ou seja