UFABC. Cálculo. Funções de Várias Variáveis. Lista 7 – Integrais Triplas. Questão 2a.
2 - A área de uma superfície determinada pelo gráfico de uma função de duas variáveis definida numa região é dada pela fórmula
Se é dada implicitamente pela equação , então
onde e supondo que nesse caso no interior de . Determine a área das seguintes superfícies:
a) A parte do plano que está no primeiro octante.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Relaxa, essa questão é um pouco confusa, mas no fim vai dar tudo certo!
Essa questão nos apresenta um modelo diferente de calcular área de uma superfície, onde
É a expressão que nos dá esse resultado.
A superfície que vamos calcular é dada pelo plano . Mas perceba que podemos escrever como , transformando assim em uma função . Assim fica no formato que precisamos pra colocar na fórmula de .
Mas como aplicamos tudo isso pra encontrar uma área? 🤔🤔
A ideia é calcular o vetor gradiente de e aplicar em .
Os limites de integração dados pela região são obtidos na projeção da superfície no plano .
Entendeu? Bora começar! 😁
Passo 2
Vamos calcular o gradiente de , lembra como é?
Derivando com relação a , temos
Já com relação a , temos
Logo seu gradiente é dado como
Calculando o modulo desse vetor, temos
Substituindo em
E nossa região , como vai ser?
Passo 3
Para obter os limites de integração vamos olhar para a base da nossa região, ou seja, quando
Sabendo que queremos a parte desse plano que fica no primeiro octante, podemos plotar essa curva e visualizar a região de forma clara.
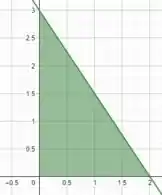
Com isso, vemos que na vertical nossa região varia da reta até . Já na horizontal, a variação ocorre entre e .
Como a variação vertical está relacionada com , os limites de são e .
Da mesma forma a variação horizontal está relacionada a , então os limites de vão de a . Com isso, nossa integral será
Agora podemos calcular nossa integral.
Bora lá!
Passo 4
Primeiro vamos integrar com relação a , como nossa função de integração é uma constante, sabemos que a integral de uma constante é a própria constante multiplicada pela variável de integração.
Aplicando os limites de integração, temos
Agora com base nesse resultado, integramos com relação a
Pelo mesmo método anterior e pelo método de integração polinomial, onde somamos na potência da variável e a dividimos pelo resultado dessa soma.
Aplicando os limites de integração
Com isso, encontramos a área da nossa superfície como !
É isso! Essa resolução te ajudou? Responde Aí! ✌