Questão 1: Calcule a integral dupla
Onde
Passo 1
Nossa primeira tarefa em integrais duplas como essa é descrever de alguma forma a região que está sendo usada para integrar a função. E assim, é uma ótima prática antes desenhar a região para entender o que fazer com essa descrição. Vamos nessa?!
A nossa região basicamente é formada pelo círculo de raio e centrado na origem:
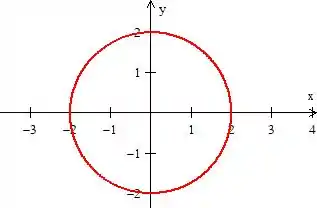
Porém, o enunciado nos delimita esse círculo dizendo que só queremos os pontos que tem . POW! é uma reta passando em e paralela ao eixo . O sinal de maior significa que vamos pegar os pontos a sua direita:
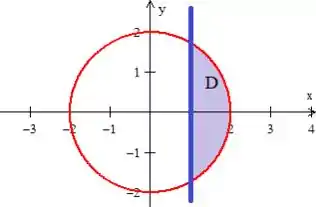
Prontinho! Essa é a nossa região !
Passo 2
Perceba que podemos descrever essa função como uma região o tipo , onde o varia em um intervalo numérico bem definido:
E o varia de uma base ao um teto:
Onde o teto representa a parte de cima do círculo, e a base, a parte de baixo...
De onde vêm essas duas partes? ORA! Da equação da circunferência que delimita o círculo...
A parte de baixo é aparte negativa da raiz, enquanto a positiva...
Passo 3
Com isso, vamos para a integral...
Para calcular essa integral aí, é válida uma mudança simples...
Mudando também os limites...
Sabemos que podemos inverter a ordem de integração se multiplicarmos por ...