- Calcule a integral abaixo
Ondeé o triangulo do plano cartesiano cujos vértices são , e .
Passo 1
Oi, galerinha! Tudo bom? Aqui temos um integralzinha para resolver, porém ele não deu os limites de integração. Só sabemos que ela está limitada na região , que é um triangulo cujos vértices são , e . Então vamos começar desenhando essa região para encontrar os limites de integração.
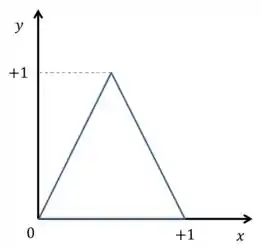
Agora vamos achar os nossos limites de integração e montar a intregal.
Passo 2
Repara que varia de até (seta horizontal) e de até também (seta vertical).
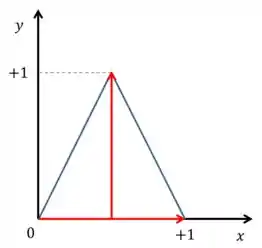
Opaaa! Com isso, nós temos os nosso limites de integração e podemos montar a nossa integral,
Agora vamos resolver a nossa integral!
Passo 3
Toda integral dupla nós sempre resolvemos de dentra para fora. Ou seja, primeiro vamos integrar em função de e depois integraremos em função de .
Integrando em função de , vamos considerar uma constante. Logo,
Substituindo os limites de integração, ficamos com
Agora intengramos em função de ,
Prontinho!