UFABC. Cálculo. Funções de Várias Variáveis. Lista 7 – Integrais Triplas. Questão 2b.
2 - A área de uma superfície determinada pelo gráfico de uma função de duas variáveis definida numa região é dada pela fórmula
Se é dada implicitamente pela equação , então
onde e supondo que nesse caso no interior de . Determine a área das seguintes superfícies:
b) A parte da superficie que está dentro do cilindro .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Essa questão parece um pouquinho difícil, não é?
A ideia dessa questão é nos mostrar uma aplicação de integrais duplas. No caso temos uma função onde e o que queremos saber é a área dessa superfície que está dentro da região limitada pelo cilindro .
Mas como vamos calcular uma área dessa forma?
Pra isso, a questão nos deu uma equação dada nesse caso por
Então o que devemos fazer é calcular o gradiente de , encontrar os limites de integração da região e calcular a integral!
Entendeu? Bora lá! 😁
Passo 2
Primeiro vamos obter o gradiente de . Lembra como que faz?
Derivando com relação a , temos
Já derivando com relação a , temos
Com isso, nosso gradiente é
Calculando o modulo desse vetor
Como na função de integração de , usamos , vamos elevar ao quadrado nosso modulo.
Sabemos que qualquer raiz de um número em que a raiz é elevada ao quadrado, resultamos no numero dentro da raiz, ou seja
Tranquilo até aqui? 😉
Passo 3
Agora vamos dar uma olhada na nossa região de integração .
Foi dito que é limitada pela equação ou seja um cilindro. Mas por agora, queremos saber a projeção desse cilindro no plano .
Pegando um cilindro na mão e olhando ele de cima, o que vemos?
Um círculo, não é?
Logo nossa região é dada por
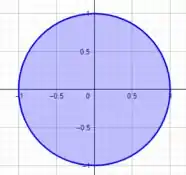
Lembre-se que se temos algo redondo na nossa região de integração, temos que usar coordenadas polares.
Os limites de integração nesse caso, são dados pelas variações do raio e do ângulo . Observando a região, vemos que a variação de vai de a . Já a variação de vai de a , já que estamos interessados em todo o círculo.
Também precisamos converter nossa função de integração para coordenadas polares também. Substituindo por , por e por , temos
Com isso, sem esquecer do jacobiano nossa integral é dada como
Bora calcular ela? 😎
Passo 4
Primeiro integrando com relação a , temos
Se aplicarmos o método de substituição onde e , logo .
Integrando pelo método polinomial, onde somamos no expoente e dividimos a variável pelo resultado da soma
Substituindo de volta, temos
Aplicando os limites de integração em
Com base nesse resultado, integramos com relação a
Passo 5
Nossa integral é
Como nossa função de integração é uma constante, então nossa integral é a própria constante multiplicada pela variável de integração
Aplicando os limites de integração, temos
Com isso, a gente encontra que a área da superfície dentro da região limitada por é igual a !
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
