Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Duplas sobre Regiões Gerais

Ver Teoria
Exercício 491234567891011121314151617181920212223242526272829303132333435363738394041424344454647485051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 2d.

2 - Esboce a região de integração e calcule as integrais iteradas a seguir

d) ∫ 0 1 ∫ x 2 x 2 x y d y d x

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão nos pediram pra esboçar a região de integração e calcular a integral de 2 x y dentro dessa região.

E agora? O que vamos fazer? 🤔

A primeira coisa que temos que fazer é analisar nossa integral

∫ 0 1 ∫ x 2 x 2 x y d y d x

Perceba que a integral com relação à y tem limites de integração x e x 2 , já para a integral com relação à x possui limites de integração 1 e 0 .

Podemos dizer que nossa região de integração é a região que está entre y = x e y = x 2 e também entre x = 1 e x = 0 ao mesmo tempo.

Está acompanhando? 👀

Passo 2

Se plotarmos essas curvas e encontrar a área que está dentro das duas variâncias, vamos ter

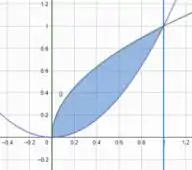
Portanto, essa é nossa região de integração!

Agora vamos calcular essa integral, vamos etapa a etapa.

Primeiro vamos integrar 2 x y com relação a y

∫ 2 x y d y

Pelo método de integração polinomial, dividimos a variável que estamos integrando pela potência da variável + 1 e somamos 1 no seu expoente.

∫ 2 x y d y = 2 x y 1 + 1 1 + 1 = x y 2

Aplicando os limites de integração nesse resultado, temos

∫ x 2 x 2 x y d y = x x 2 - x x 2 2

∫ x 2 x 2 x y d y = x 2 - x 5

Tranquilo até aqui? 😁

Passo 3

A partir desse resultado, vamos integrar com relação a x . Como sabemos que a integral da soma é a soma das integrais, temos

∫ x 2 - x 5 d x = ∫ x 2 d x - ∫ x 5 d x

Também por integração de polinômios, vamos obter

∫ x 2 d x = x 2 + 1 2 + 1 = x 3 3

∫ x 5 d x = x 5 + 1 5 + 1 = x 6 6

Substituindo na integral da soma e aplicando os limites de integração

∫ x 2 - x 5 d x = x 3 3 - x 6 6

∫ 0 1 ∫ x 2 x 2 x y d y d x = ∫ 0 1 x 2 - x 5 d x = 1 3 3 - 1 6 6 - 0 3 3 - 0 6 6

∫ 0 1 ∫ x 2 x 2 x y d y d x = 1 6

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

∫ 0 1 ∫ x 2 x 2 x y d y d x = 1 6

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x